Wykres funkcji – dwuznaczne pojęcie matematyczne:
- dla dowolnych zbiorów i funkcji między nimi jej wykresem nazywa się zbiór par uporządkowanych dany wzorem[2]:
- innymi słowy wykres tworzą pary złożone z argumentu i odpowiedniej wartości;
- wykres funkcji to także przedstawienie jej graficznie, prezentując powyższy zbiór lub jego część[3]. Jest to możliwe tylko dla niektórych funkcji, o odpowiedniej dziedzinie i przeciwdziedzinie, m.in. dla przypadków opisanych niżej.
Sens mnogościowy
[edytuj | edytuj kod]Rzeczywiste argumenty i wartości
[edytuj | edytuj kod]W pierwszym wypadku argumenty funkcji i jej wartości mogą być między innymi liczbami rzeczywistymi. W szczególności – jeśli to funkcja jest nazywana funkcją rzeczywistą jednej zmiennej rzeczywistej. Jej wykresem są wszystkie punkty postaci gdzie oraz Jest to podzbiór płaszczyzny kartezjańskiej, którą da się utożsamić z płaszczyzną euklidesową. Wzajemną odpowiedniość (bijekcję) zapewnia tu dowolny układ współrzędnych kartezjańskich[4][5].
Argumenty funkcji i jej wartości mogą też należeć do innych zbiorów, np. wielowymiarowych przestrzeni kartezjańskich. Zbiór wszystkich par oznacza się i nazywa się iloczynem kartezjańskim. Jeśli to dowolną funkcję nazywa się funkcją dwóch zmiennych rzeczywistych. Jeśli to wykresem funkcji rzeczywistej są wtedy wszystkie punkty postaci[6]:
Taka funkcja to inaczej pole skalarne na płaszczyźnie kartezjańskiej lub jej fragmencie. Funkcje tego typu można przedstawiać na co najmniej trzy sposoby – figurami dwu- lub trójwymiarowymi, co pokazują ilustracje obok.
W ogólności, gdy to:
Przypadek ogólny
[edytuj | edytuj kod]Wykresy rozumiane w ten sposób – jako podzbiory odpowiednich iloczynów kartezjańskich – to jednoznaczne relacje dwuczłonowe między dziedziną funkcji a przeciwdziedziną swojej funkcji. Takie pojęcie wykresu pokrywa się z jedną z formalnych definicji samej funkcji – definicją Peana[7].
Sens graficzny
[edytuj | edytuj kod]

Informacje ogólne
[edytuj | edytuj kod]Jak wspomniano wyżej, wykresy rozumiane graficznie są możliwe tylko dla niektórych funkcji, o odpowiednich dziedzinach i przeciwdziedzinach. Jeśli to wykres jest możliwy m.in. dla funkcji:
- rzeczywistych jednej zmiennej rzeczywistej:
- rzeczywistych dwóch zmiennych rzeczywistych:
- zespolonych jednej zmiennej rzeczywistej:
- zespolonych jednej zmiennej zespolonej:
Funkcje rzeczywiste jednej zmiennej rzeczywistej
[edytuj | edytuj kod]Wykresy takich funkcji najczęściej są przedstawiane w kartezjańskim układzie współrzędnych[3]. Jednoznaczność funkcji jest związana z pewną własnością geometryczną takiego wykresu. Każda prosta pionowa – tj. równoległa do osi wartości – przecina taki wykres co najwyżej raz[8][9]. Widać to na jednej z ilustracji – niebieski wykres rozkładu normalnego jest przecinany przez szare, pionowe linie i każda z nich przecina wykres dokładnie raz.
Wykres takiej funkcji nie musi być krzywą – może:
- być układem rozłącznych krzywych – por. wykresy funkcji signum, podłogi i sufitu;
- w ogóle nie zawierać krzywych – por. wykresy funkcji Dirichleta i funkcji Riemanna.
Z takiego wykresu da się odczytać podstawowe własności funkcji:
- dziedzina funkcji – ta część osi argumentów, która jest nad wykresem, pod nim lub się z nim pokrywa; dziedzina funkcji to rzut prostokątny wykresu na oś argumentów;
- miejsca zerowe – przecięcia wykresu z osią argumentów;
- punkty ekstremalne;
- punkty osobliwe;
- monotoniczność;
- okresowość.
Funkcje rzeczywiste dwóch zmiennych rzeczywistych
[edytuj | edytuj kod]Niech dziedzina funkcji będzie obszarem na płaszczyźnie euklidesowej. Jeśli ta funkcja jest ciągła, to jej wykres jest powierzchnią[6]; przykłady podano na ilustracjach. Powierzchnia wykresu może być „zawieszona” nad tym obszarem, pod nim lub go przecinać.
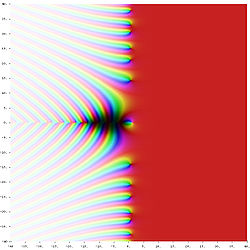
Funkcje zespolone
[edytuj | edytuj kod]Zobacz też
[edytuj | edytuj kod]Przypisy
[edytuj | edytuj kod]- ↑
 Jan Pluta, Krzywa Gaussa i odchylenie standardowe, zpe.gov.pl [dostęp 2025-08-05].
Jan Pluta, Krzywa Gaussa i odchylenie standardowe, zpe.gov.pl [dostęp 2025-08-05].
- ↑ Leksiński, Nabiałek i Żakowski 1995 ↓, s. 46.
- ↑ a b wykres funkcji, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2025-08-03].
- ↑
 Wykres i miejsce zerowe funkcji, Matematyka z ZUT-em, Zachodniopomorski Uniwersytet Technologiczny w Szczecinie (ZUT), matematyka.zut.edu.pl [dostęp 2025-08-05].
Wykres i miejsce zerowe funkcji, Matematyka z ZUT-em, Zachodniopomorski Uniwersytet Technologiczny w Szczecinie (ZUT), matematyka.zut.edu.pl [dostęp 2025-08-05].
- ↑
 Anna Barbaszewska-Wiśniowska, Funkcje jednej zmiennej rzeczywistej. Wykres funkcji, serwis Open AGH, Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie, epodreczniki.open.agh.edu.pl [dostęp 2025-08-05].
Anna Barbaszewska-Wiśniowska, Funkcje jednej zmiennej rzeczywistej. Wykres funkcji, serwis Open AGH, Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie, epodreczniki.open.agh.edu.pl [dostęp 2025-08-05].
- ↑ a b Krysicki i Włodarski 2006 ↓, s. 17.
- ↑
 Anna Barbaszewska-Wiśniowska, Pojęcie funkcji. Dziedzina i przeciwdziedzina, Open AGH, epodreczniki.open.agh.edu.pl [dostęp 2025-08-05].
Anna Barbaszewska-Wiśniowska, Pojęcie funkcji. Dziedzina i przeciwdziedzina, Open AGH, epodreczniki.open.agh.edu.pl [dostęp 2025-08-05].
- ↑ Eric W. Weisstein, Vertical Line Test, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-08-05].
- ↑ Krysicki i Włodarski 1994 ↓, s. 64.
Bibliografia
[edytuj | edytuj kod]- Włodzimierz Krysicki, Lech Włodarski: Analiza matematyczna w zadaniach. Wyd. XXI. T. 1. Warszawa: Wydawnictwo Naukowe PWN, 1994. ISBN 83-01-01460-1.
- Włodzimierz Krysicki, Lech Włodarski: Analiza matematyczna w zadaniach. Wyd. 27. T. 2. Warszawa: Wydawnictwo Naukowe PWN, 2006. ISBN 978-83-01-14296-4.
- Wacław Leksiński, Ireneusz Nabiałek, Wojciech Żakowski: Matematyka. Definicje, twierdzenia, przykłady, zadania. Wyd. V. Warszawa: Wydawnictwa Naukowo-Techniczne, 1995, seria: Podręczniki akademickie: elektronika, informatyka, telekomunikacja. ISBN 83-204-1892-5.
Linki zewnętrzne
[edytuj | edytuj kod] Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej (ZPE MEN), zpe.gov.pl [dostęp 2025-08-04]:
Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej (ZPE MEN), zpe.gov.pl [dostęp 2025-08-04]:
- Anna Jeżewska, Wykres funkcji i wykresy wybranych funkcji;
- Witold Sadowski, Paweł Kwiatkowski, Czytanie wykresu funkcji;
- Jan Pluta, Jak czytać wykresy i schematy?;
- Hanna Mąka, Szkicowanie wykresów funkcji o zadanych własnościach;
- Katarzyna Podfigurna, Zastosowanie wykresów funkcji do rozwiązywania zadań.
- Eric W. Weisstein, Function Graph, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-08-03].
 Graph of a mapping (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2025-08-03].
Graph of a mapping (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2025-08-03].