Enkel funktion

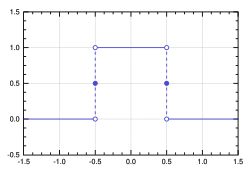
En enkel funktion är inom matematisk analys en funktion som endast antar ett ändligt antal värden. Ett enkelt exempel är takfunktionen på intervallet ${\displaystyle [0,9]}$ som endast antar värden ${\displaystyle \{0,1,2,3,4,5,6,7,8,9\}}$. Ett annat exempel är Dirichlets funktion som endast antar värden 0 (för irrationella tal) och 1 (för rationella tal). Enkla funktioner används i första stadiet av konstruktionen av exempelvis Lebesgueintegralen, då det är väldigt lätt att integrera över en enkel funktion.

Definition

En enkel funktion kan uttryckas som en linjärkombination av indikatorfunktioner, ${\displaystyle \chi _{A_{k}}}$, av mätbara mängder. Om ${\displaystyle (X,F)}$ är ett mätbart rum, ${\displaystyle A_{1},A_{2},...,A_{n}}$ är en följd av mätbara mängder och ${\displaystyle a_{1},a_{2},...,a_{n}}$ en följd av tal, är

${\displaystyle f(x)=\sum _{k=1}^{n}a_{k}\chi _{A_{k}}(x)}$

en enkel funktion.

Egenskaper

Summor, skillnader och produkter av enkla funktioner är återigen enkla funktioner, så att mängden av alla enkla funktioner bildar en kommutativ algebra över en kropp.

För varje icke-negativ mätbar funktion f från ett måttrum X till de reella talen existerar det en följd av enkla funktioner ${\displaystyle 0\leq s_{1}\leq s_{2}\leq ...\leq f}$ så att

${\displaystyle s_{n}(x)\to f(x)}$

likformigt när ${\displaystyle n\to \infty }$.

Integration

Om ${\displaystyle (X,F,\mu )}$ är ett måttrum, så är integralen av en enkel funktion ${\displaystyle f}$ med avseende på ${\displaystyle \mu }$:

${\displaystyle \int f\,d\mu =\sum _{k=1}^{n}a_{k}\mu (A_{k})}$

om alla summander är ändliga.

Referenser

• Walter, Rudin (1987). Real and Complex Analysis. McGraw-Hill. ISBN 0-07-100276-6