RLC kolo

RLC kolo je električno kolo koje se sastoji od otpornika (R), induktora (L) i kondenzatora (C) povezanih redno ili paralelno. Ime RLC je dobijeno tako što se tim slovima označavaju vrednosti otpora, induktivnosti i kapacitivnosti. Ovo električno kolo čini harmonijski oscilator za struju i oscilovaće na sličan način kao LC kolo. Glavna razlika je u tome što prisustvo otpornika čini da bilo koja oscilacija koja se indukuje u kolu nestane tokom vremena ukoliko izvor ne nastavi sa radom. Ovaj efekat otpornika se zove prigušivanje. Prisustvo otpornosti takođe malo smanjuje maksimalnu rezonantnu frekvenciju. Otpor je neizbežan u realnim električnim kolima, iako otpornik nije u električnom kolu kao posebna komponenta. Idealno čisto LC kolo je apstrakcija čisto za potrebe teorije.
Postoji mnogo primena za ovakav tip kola. Koriste se u raznim vrstama oscilatornih kola. Druga bitna primena je u tjunerima, kao što su radio prijemnici ili televizori, gde se koriste kako bi se odabrao uzak opseg frekvencija iz okolnih radio talasa. U ovoj ulozi, kolo se često naziva tjunovano kolo. RLC kolo može da se koristi kao visoko propusni filtar, nisko propusni filtar, ograničen propusni filtar. Primena u tjuner kolu predstavlja ograničen propusni opseg. RLC filtar se opisuje kao kolo drugog reda, što znači da bilo koja napon ili struja u kolu mogu da se opišu preko diferencijalnih jednačina drugog reda u analizi električnih kola.
Tri elementa kola mogu da se kombinuju u različite topologije. Sva tri elementa povezana redno ili paralelno su najjednostavniji koncept i najlakši za analizu. Postoje i druge topologije koje imaju praktičan značaj. Jedan problem koji se često sreće je da je potrebno uračunati vrednost otpora kalema. Kalemi se uglavnom prave od zavojaka žice, koja ima često nepoželjan otpor, i uglavnom ima značajan efekat u električnom kolu.
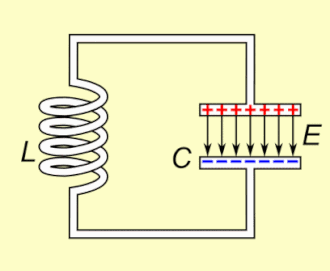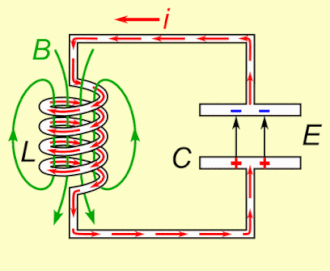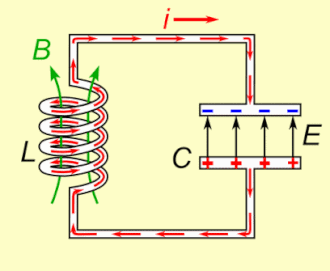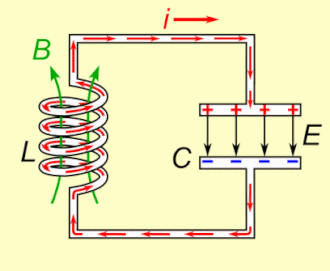
Osnovni principi
Rezonanca
Značajna osobina ovog kola je mogućnost da osciluje na određenoj frekvenciji, rezonantna frekvencija, . Frekvencija se meri u jedinici Herc. U ovom članku će se koristiti ugaona frekvencija, , koja je pogodnija za matematička izračunavanja. Meri se u radijanima u sekundi. Međusobno su povezane prostom jednakošću,
Rezonancija se javlja zato što se energija čuva na dva različita načina: u električnom kada se kondenzator puni i u magnetnom polju kada struja prolazi kroz kalem. Energija može da se prebacuje iz jedne u drugu u okviru ovog kola i to prebacivanje može da bude oscilatorno. Mehanička analogija je teg koji je ovešen o oprugu i koji osciluje gore-dole kada se pusti. Ovo nije samo metafora; teg na opruzi se opisuje potpuno istom diferencijalnom jednačinom drugog reda pošto za RLC kolo i sva svojstva mehaničkog sistema postoje analogne vrednosti. Mehaničko svojstvo koje odgovara otporniku u kolu je trenje u opruga/teg sistemu. Trenje će polako zaustaviti svako oscilovanje ako ne postoji spoljna sila koja dodaje energiju. Isto tako, otpor u RLC koli će "prigušiti" oscilacije, koje će vremenom oslabiti ukoliko ne postoji izvor naizmenične struje u kolu.
Rezonantna frekvencija je definisana kao frekvencija na kojoj je električna impedansa kola u svom minimumu. Ekvivalentno, može da se definiše kao frekvencija na kojoj je impedansa čisto realna vrednost (tj. čist otpor). Ovo se dešava zato što su impedanse kalema i kondenzatora na rezonantoj frekvenciji jednake ali suprotnog znaka i one se neutrališu. Električna kola gde su kalem i kondenzator paralelno povezani umesto redno će imati makcimumalnu impedansu umesto minimalne. Zbog ovoga se često nazivaju antirezonatorima, mada se i dalje frekvencija na kojoj se to dešava zove rezonantna frekvencija.
Prirodna frekvencija
Rezonantna frekvencija je definisana u pogledu impedanse koju vidi izvor energije. Moguće je da kolo nastavi za oscilovanjem neko vreme nakon što se izvor isključi ili ukoliko se napon izvora naglo promeni na nulu. Ovo je slično načinu na koji zvučna viljuška nastavlja sa zvonjavom nakon udarca, i taj efekat se često zove zvonjava. Ovaj efekat je maksimalna prirodna vrednost frekvencije električnog kola i generalno nije ista kao i rezonancija kola koja nastaje povezivanjem kola sa izvorom, mada su često vrlo bliske. Različiti termini se koriste od strane različitih autora za razlikovanje ovih frekvencija, ali rezonatna frekvencija obično podrazumeva rezonanciju usled povezivanja sa izvorom. Ona takođe može da se zove neprigušenom rezonancijom ili neprigušenom prirodnom frekvencijom a maksimalna vrednost frekvencije može da se zove i prigušenom rezonantnom frekvencijom ili prigušenom prirodnom frekvencijom. Razlog za ovu terminologiju je taj što rezonantna frekvencija usled povezivanja sa izvorom u rednom ili paralelnom rezonantnom kolu ima vrednost[1]
Ovo je potpuno ista vrednost kao i za rezonantnu vrednost LC kola, tj., RLC kola bez otpornika, tj. , ista je kao i za kolo u kome nema prigušivanja, zato se i nazova neprigušena rezonantna frekvencija. Maksimalna rezonantna frekvencija, sa druge strane, zavisi od vrednosti otpornika i opisuje se kao prigušena rezonantna frekvencija. Visoko prigušeno kolo će potpuno prestati sa rezonancijom kada nema priključen izvor. Kolo sa vrednošću otpornika koji čini da kolo bude na ivici zvonjave se naziva kritično prigušeno. Dve strane od tačke kritičnog prigušenja se nazivaju premalo prigušene (dešava se zvonjenje) ili previše prigušena (zvonjenje je potisnuto).
Električna kola sa komplikovanijim topologijama od redne ili paralelne veze (neka od njih su opisana kasnije) imaju rezonantnu frekvenciju koja nastaje povezivanjem na izvor koja odudara od i za njih neprigušena rezonantna frekvencija, prigušena rezonantna frekvencija i rezonatna frekvencija usled povezanosti sa izvorom mogu sve biti različite.
Prigušivanje
Prigušivanje nastaje zbog otpora u kolu. Ono određuje da li će kolo prirodno oscilovati (bez priključenog izvora) ili ne. Kola koja osciluju na ovaj način se opisuju kao premalo prigušena, dok se kola koja ne osciluju na ovaj način nazivaju previše prigušena. Smanjenje prigušivanja (simbol α) se meri u niprima u sekundi. Ali često pogodnija mera je faktor prigušivanja (simbol ζ, zeta)koji je bez jedinica i povezan je sa α na sledeći način:
Specijalni slučaj kada je ζ = 1 , zove se kritično prigušivanje i predstavlja slučaj kada je kolo na ivici oscilovanja. Ovo je minimalno priguššivanje koje može da se primeni bez izazivanja oscilovanja.
Frekventni opseg
Efekat rezonancije može da se koristi za filtriranje, nagla promena impedanse blizu rezonancije može da se koristi za propuštanje ili blokiranje signala koji su blizu rezonantne frekvencije. Mogu da se naprave filtri sa propuštanjem i blokiranjem određenih frekvencija i neki su prikazani kasnije u članku. Ključan parametar u dizajniranju filtara je frekventni opseg. Frekventni opseg se meri između 3dB-tačaka, tj. , frekvencije na kojima je snaga koja prolazi kroz kolo smanjena duplo u odnosu na rezonantnu frekvenciju. Postoje dve frekvencije sa duplo manjom snagom, jedna iznad, i jedna ispod rezonantne frekvencije:
gde je frekventni opseg, je donja frekvencija sa duplo manjom snagom je gornja frekvencija sa duplo manjom snagom. Frekventni opseg je povezan sa prigušivanjem na sledeći način:
gde su jedinice radijani u sekundi, respektivno. Druge jedinice mogu da zahtevaju faktor konverzije. Uopštenija mera frekventnog opsega je deo frekventnog opsega koji izražava frekventni opseg kao deo rezonatne frekvencije i dat je sa:
Deo frekventnog opsega se često naziva procentom. Prigušivanje filtara se podešava kako bi odgovaralo projektovanom frekventnom opsegu. Uski filtri kao što je noč filtar, zahtevaju malo prigušivanje. Filtar širokog opsega zahteva veće prigušivanje.
Q faktor
Q faktor je široko rasprostranjena mera koja se koristi za opis rezonantnih kola. Definisana je kao maksimalna energija koja se čuva u kolu podeljena prosečnom energijom koja se predaje u kolu po ciklusu rezonancije. Mala Q kola su zbog toga prigušena i kola sa velikim Q su premalo prigušena. Q je povazana sa frekventnim opsegom; mala Q kola su širokog opsega, a velika Q kola su uskog opsega. U stvari, dešava se da je Q obrnuta vrednost dela frekventnog opsega:
Q faktor je srazmeran sa selektivnošću, zato što Q faktor zavisi obrnuto srazmerno od frekventnog opsega.
Skalirani parametri
Parametri ζ, Fb, i Q su svi skalirani na ω0. Ovo znači da kola koja imaju slične parametre dele slične karakteristike nezavisno od toga da li rade u istom frekventnom opsegu.
Sledeće poglavlje daje detaljnu analizu rednog RLC kola. Druge topologije nisu opisane toliko detaljno, ali su opisane glavne razlike u odnosu na redno kolo. Uopšten oblik diferencijalnih jednačina koji je predstavljen u poglavlju sa rednim kolom je primenljiv za sva kola drugog reda i može da se koristiza opis napona ili struje u bilo kom elementu kola.
Redno RLC kolo
 |
Slika 1: RLC redno kolo |
|
U ovom kolu, tri komponente su povezane redno sa naponskim izvorom. Glavna diferencijalna jednačina može da se dobije zamenom konstitutivnih jednačina za svaki od tri elementa u Drugi Kirhofov zakon. Iz Drugog Kirhofovog zakona,
gde su naponi na R, L and C respektivno i je vremenski promenljiv napon od izvora. Zamenom u konstitutivne jednačine:
Za slučaj gde je izvor nepromenljivog napona, izvod i podela sa L daju diferencijalne jednačine drugog reda:
Ovo može da se korisno predstavi u primenljivijem i opštijem obliku:
and su jedinice ugaone frekvencije. se zove "nipr frekvencija" ili "prigušivanje", i mera je koliko brzo tranzijentni odziv nestaje nakon uklanjanja izvora. je ugaona rezonantna frekvencija.[2]
Za slučaj rednog RLC kola data su dva parametra:[3]
- i
Koristan parametar je "faktor prigušivanja", koji je definisan kao odnos,
U slučaju rednog RLC kola, faktor prigušivanja je dat kao,
Vrednost faktora prigušivanja određuje tip tranzijenata koje će kolo napraviti.[4] Neki autori ne koriste i zovu faktorom prigušivanja.[5]
Tranzijentni odziv

Diferencijalna jednačina za kolo se rešava na tri različita načina u zavisnosti od vrednosti . Za slabo prigušena kola (), previše prigušena kola () i kritično prigušena ().
Koreni jednačine u s su,
Opšte rešenje diferencijalne jednačine je eksponencijalno za bilo koji koren ili linearna superpozicija oba korena,
Koeficijenti A1 i A2 su određeni sa graničnim stanjem specifičnog problema koji se analizira. Tj., dobijaju vrednosti koje zavise od struja i napona u kolu pre početka tranzijenta i pretpostavljene vrednosti u koju će se vratiti sistem nakon beskonalno mnogo vremena.[6]
Previše prigušen sistem
Odziv previše prigušenog sistema () je,[7]
Odziv previše prigušenog sistema je opadanje tranzijentne struje bez oscilacija.[8]
Premalo prigušen sistem
Odziv premalo prigušenog sistema () je,[9]
Primenjujući standarne trigonometrijske identitete, dve trigonometrijske funkcije mogu da se izraze kao jedna sinusoida sa faznim pomakom,[10]
Odziv premalo prigušenog sistema je oscilacija koja slabi na frekvenciji . Oscilacija slabi brzinom koje je određena prigušenjem . Eksponencijalna vrednost u opisuje oblik oscilacija. B1 i B2 (ili B3 i fazni pomak u drugom obliku) su proizvoljne konstante određene graničnim uslovima. Frekvencija je data sa,[9]
Ovo se zove prigušena rezonantna frekvencija ili prigušena prirodna frekvencija. To je frekvencija na kojoj će kolo prirodno oscilovati ako nije napajano spoljnim izvorom. Rezonantna frekvencija, , koja je frekvencija na kojoj kolo osciluje kada je napajano spoljnom oscilacijom, se često zove neprigušenom rezonantnom frekvencijom da bi se razlikovalo.[11]
Kritično prigušen odziv
Kritično prigušen odziv () jednak je,[12]
Kritično prigušen odziv predstavlja odziv kola kome najvećom mogućom brzinom slabi signal, bez oscilatornog ponašanja. Ova činjenica je bitna u kontrolnim sistemima gde se zahteva brzo dostizanje određenog stanja bez premašivanja.D1 i D2 su proizvoljne konstante određene graničnim uslovima.[13]
Laplasova oblast
Redno RLC kolo može da se analizira za tranzijentna i nepromenljiva naizmenična kola koristeći Laplasove transformacije.[14] Ako naponski izvor proizvodi naponski signal sa Laplasovo-transformisanim V(s) (gde jes kompleksna frekvencija ), Drugi Kirhofov zakon može da se primeni u Laplasovoj oblasti:
gde je I(s) Laplasovo-transformisana struja kroz sve komponente. Rešavajući po I(s):
I preuređivanjem, dobija se
Laplasova admitansa
Rešavajući za Laplasovu admitansu Y(s):
Uprošćavajući korišćenjem parametara α i ωo definisanih u prethodnoj sekciji, dobijamo
Kompleksna reprezentacija
Kompleksna analiza nula Y(s) su vrednosti s takve da važi :
Polovi od Y(s) su vrednosti s takve da . Kvadratnom jednačinom, dobija se
Polovi Y(s) su identični korenima i karakteristične polinomne ili diferencijalne jednačine u skcijama oznad.
Opšte rešenje
Za proizvoljno E(t), rešenje koje se dobija inverznom transformacijom I(s) je:
gde je , i cosh i sinh su uobičajene hiperboličke funkcije.
Ravnotežno stanje
Sinusoidno ravnoteđno stanje je predstavljeno dodeljujući
Uzimajući intenzitet gornje jednačine i zamenjujući ispod,
i struju koja je funkcija ω može da se pronađe iz,
Maksimalna vrednost je . Vrednost ω u ovom maksimumu je, u ovom slučaju, jednaka neprigušenoj prirodnoj rezinanciji:[15]
Paralelno RLC kolo
 |
| Figure 5. RLC paralelno kolo |
|
Osobine paralelnog RLC kola mogu da se dobiju iz dualnog odnosa električnih kola i razmatranjem da je paralelno RLC kolo dualna impedansa rednog RLC kola. Uzimajući ovo, postaje jasno da su diferencijalne jednačine koje opisuju ovo kolo identične opštoj formi onih koje opisuju redno RLC kolo.
Za paralelno kolo, prigušivanje α je dato sa[16]
i faktor prigušenja je
Ovo je suprotna vrednost izraza za ζ u rednom kolu. Isto tako, ostali parametri, deo frekventnog opsega i Q su inverzni jedan drugom. Ovo znači da filtar širokog opsega sa malom Q vrednošću u jednoj topologiji postaje filtar uskog frekventnog opsega i velike Q vrednosti u drugoj topologiji kada se naprave od istih komponenti sa identičnim vrednostima. Q i deo frekventnog opsega paralelnog kola su dati sa:
Frekventni domen

Kompleksne admitanse ovog kola su dobijene dodavanjem admitansi komponenata:
Promena od rednog povezivanja na paralelno rezultuje u kolu koje ima maksimalnu vrednost impedanse na rezonantnoj frekvenciji umesto minimuma, tako da kolo postaje antirezonantno.
Grafik pokazuje da postoji minimum struje u frekventnom odzivu na rezonantnoj frekvenciji kada je kolo napajano konstantnim naponom. Sa druge strane, ako je izvor konstantne struje, postojaće maksimum napona koji će pratiti istu krivu kao i struja u rednom kolu.
Druge konfiguracije


Redno povezan otpor sa kalemom u paralelnom LC kolu kao što je prikazano na slici 7 , je topologija koja se često sreće kada je potrebno uneti u račun otpor kalema. Paralelna LC kola se često koriste za filtre sa određenim propusnim opsegom i Q najviše zavisi od ove otpornosti. Rezonantna frekvencija kola je,[17]
Ovo je rezonantna frekvencija kola definisana na frekvenciji na kojoj admitansa ima imaginarni deo jednak nuli. Frekvencija koja se pojavljuje u opštem obliku karakteristične jednačine (koja je ista za ovo kolo kao i za prethodno),
nije ista frekvencija. U ovom slučaju to je prirodna neprigušena rezonantna frekvencija [18]
Frekvencija na kojoj je makcimalna vrednost impedanse je data sa,[19]
gde je faktor kvaliteta kalema. Ovo može da se aproksimira sa,[19]
- .
Dalje, tačna maksimalna vrednost impedanse je data sa,[19]
- .
Za vrednosti veće od jedinične, ovo može dobro da se aproksimira sa,[19]
- .
Takođe, otpornik u paraleli sa kondenzatorom u rednom LC kolu može da se iskoristi za predstavljanje kondenzatora sa dielektrikom sa gubicima. Ova konfiguracija je prikazana na slici 8. Rezonantna frekvencija (frekvencija na kojoj admitansa ima imaginarni deo jednak nuli) u ovom slučaju je data sa,[20]
dok je frekvencija na kojoj je impedansa maksimalna data sa
gde je
Istorija
Prvi dokaz da kondenzator može da proizvede električne oscilacije je otkriven 1826. od strane francuskog naučnika Feliksa Savara.[21][22] On je otkrio da Lajdenova tegla koja se prazni kroz žicu namotanu oko gvozdene igle, ponekada ostavi iglu namagnetisanu u jednom smeru, a ponekad u drugom. On je tačno zaključio da se ovo dešava zbog prigušeno oscilatorne struje pražnjenja u žici, koja je okretala namagnetisanje igle napred-nazad dok nije postalo suviše malo da bi imalo efekta, ostavljajući iglu namagnetisanu u slučajnom smeru.
Američki fizičar Džozef Henri je ponovio Savarov eksperiment 1842. i došao do istog zaključka, navodno nezavisno.[23][24] Britanski naučnik Vilijam Tompson je 1853. pokazao matematički da pražnjenje Lajdenove tegle kroz kalem treba da bude oscilatorno, i izveo je rezonantnu frekvenciju.[21][23][24]
Briitanski radio istraživač Oliver Lodž, je pražnjenjem Lajdenovih tegli kroz dugačku žicu napravio kolo podešeno na svoju rezonantnu frekvenciju u audio opsegu, koja je proizvodila muzičku notu iz varnice prilikom pražnjenja.[23] 1857. Nemački fizičar Berend Vilhelm Federsen je fotografisao varnicu nastalupražnjenjem Lajdenove tegle pomoću rotirajućeg ogledala i time je predstavio vidljiv dokaz oscilacija.[21][23][24] 1868. Škotski fizičar Džejms Klark Maksvel je izračunao efekat primene naizmenične struje kolu sa kalemom i kondenzatorom, pokazujući da je odziv maksimalan na rezonantnoj frekvenciji.[21]
Prvi primer krive električne rezonancije je objavljen 1887. od strane nemačkog naučnika Hajnriha Herca i njegovom pionirskom radu na otkiruću radio talasa, pokazujući dužinu varnice koju je dobio pomoću svog LC rezonator detektora prema frekvenciji.[21]
Jedna od prvih demonstracija rezonancije između podešenih kola je bio Lodžov eksperiment oko 1889.[21][23] On je postavio dva rezonantna kola jedno pored drugog, svako se sastojalo od Lajdenove tegle povezane sa podesivim kalemom sa jednim zavojkom i vazdušnim razmakom preko koga se stvarala varnica. Kada je visok sa indukcionog kalema primenjen na jedno kolo, stvarajući varnice i samim tim oscilujuću struju, varnice su se javile na drugom kraju ukoliko su oba kalema bila naštelovana na rezonanciju. Lodž i neki Engleski naučnici su preferirali termin "sintoni" za ovaj efekat, ali se termin rezonancija zadržao.[21]
Prva praktična primena za RLC kola je bila 1890. u radio predajnicima sa preskačućom varnicom koja je omogućavala prijemniku da se podesi na istu frekvenciju kao i predajnik. Ovaj prvi patent na radio sistem koji je omogućavao tačno nameštanje frekvencije je predstavio Lodž 1897., iako su prvi praktični sistemi izmišljeni 1900. od strane ango-italijanskog naučnika Markonija.[21]
Primena
Promenljivo podešavajuća kola
Veoma česta primena ovih kola je u tjunerima radio prijemnika. Podesivo podešavanje frekvencije se uglavnom ostvaruje preko promenljivog kondenzatora sa paralelnim pločama koji omogućava da se vrednost kapacitivnosti menja i time da se odaberu radio stanice različite frekvencije. Za deo radia gde se fabrički podešava frekvencija, pogodniji su kalemi sa podesivim jezgrom čime se menja induktivnost. U ovom dizajnu, jezgro je napravljeno od materijala sa velikom permeabilnošću koje ima efekat povećavanja induktivnosti. Jezgro ima navoj tako da može da se ušrafi dublje ili pliće u navojke kalema.
Filtri
 |  |
 |  |
 |  |
U primenama filtriranja, otpornik R postaje opterećenje prema kome radi filtar. Vrednost faktora prigušenja je izabrana prema željenom frekventnom opsegu filtara. Za veći opseg, bira se veća vrednost faktora prigušivanja (i suprotno). Tri komponente daju dizajneru tri stepena slobode. Dva stepena slobode su neophodna za odabirfrekventnog opsega i rezonantne frekvencije. Dizajner i dalje ima jedan stepen slobode koji može da se iskoristi da se skaliraju R, L i C na praktične vrednosti. Alternativno, R može da bude predodređeno spoljnim kolom koje će koristiti poslednji stepen slobode.
- Filtar koji propušta niske frekvencije
RLC kolo može da se koristi kao filtar koji propušta niske frekvencije. Konfiguracija ovog kola je prikazana na slici 9. Frekvencija krivine, tj. frekvencija na 3dB tački, je data sa
Ovo je takođe frekventni opseg filtara. Faktor prigušivanja je dat sa[25]
- Filtar koji propušta visoke frekvencije
Filtar koji propušta visoke frekvencije je prikazan na slici 10. Frekvencija krivine je ista kao za filtar koji propušta niske frekvencije
Filtar ima stop opseg ove širine.[26]
- Filtar koji propušta određeni opseg frekvencija
Filtar koji propušta određeni opseg frekvencija može da se napravi od RLC kola ili stavljanjem LC kola u rednu vezu sa otpornikom ili stavljanjem LC kola koje je paralelno povezano sa otponikom. Ove topologije su pokazane na slikama 11 i 12. Centralna frekvencija je data sa:
i frekventni opseg za redno kolo je [27]
Verzija kola sa paralelno povezanim kolom je namenjena da se napaja izvorom visoke impedanse, tj. , strujnim izvorom. Pod tim uslovima opseg je [27]
- Filtar koji ne propušta određeni opseg
Slika 13 pokazuje filtar koji ne propušta određeni opseg napravljen pomoću paralelno povezanog LC kola redno sa otporom. Prvi slučaj zahteva izvor visoke impedanse da bi se struja preusmerila u rezonator gde postaje mala impedansa na rezonanciji. Drugi slučaj zahteva izvor male impedanse tako da napon pada preko antirezonatora kada postaje visoka impedansa na rezonanciji.[28]
Oscilatori
Za primene u oscilatornim kolima, obično je poželjno napraviti prigušivanje (ili ekvivalentno, faktor prigušenja) najmanjim mogućim. U praksi, ova osobina zahteva pravljenje otpora kola R najmanje fizički mogućim za redno kolo, ili alternativno povećavajući R na najvišu moguću vrednost za paralelno kolo. U svakom slučaju, RLC kolo postaje dobra aproksimacija idealnom LC kolu. Ipak za kola sa veoma malim prigušivanjem (veliki Q-faktor) , problemi kao što su dielektrični gubici kondenzatora i kalema mogu postati značajni.
U oscilatornom kolu
ili ekvivalentno
Kao rezultat
Množač napona
U rednom RLC kolu na rezonanciji, struja je ograničena samo otporom u kolu
Ako je R malo, i sastoji se npr. samo od otpora zavojka kalema, onda će ova struja biti velika. Napon na kalemu će biti
Ista vrednost napona će da se javi i na kondenzatoru u suprotnoj fazi od kalema. Ako R može da se napravi dovoljno malim, ovi naponi mogu da budu nekoliko puta veći od ulaznog napona. Odnos napona je, u osnovi, Q kola,
Sličan efekat se posmatra strujama u paralelnim kolima. Iako kolo deluje kao visoka impedansa spoljnom izvoru, postoji velika struja koja cirkuliše u unutrašnjoj konturi koja se sastoji od paralelnog kalema i kondenzatora.
Kola sa pulsnim pražnjenjem
Previše prigušena redna RLC kola mogu da se koriste kao pulsna struja pražnjenja. Često je korisno znati vrednosti komponenata koja mogu da proizvedu ovaj signal i opisana su formulom:
Takvo kolo mođe da se sastoji od kondenzatora koji čuva energiju, otpornika, nekog kalema i prekidača, svi povezani redno. Početni uslovi su takvi da je kondenzator na naponu i ne postoji struja kroz kalem. Ako je induktivnost poznata, onda su preostali parametri zadati na sledeći način - kapacitivnost:
Otpor (ukupan od kola i opterećenja):
Inicijalna maksimalna vrednost kondenzatora:
Prebacivajući u oblik gde je R poznato – kapacitivnost je:
Induktivnost je (ukupna od kola i opterećenja):
Početna maksimalna vrednost napona kondenzatora:
Vidi još
- RC kolo
- LC kolo
- RL kolo
- Elektronski oscilator
- Kirhofovi zakoni
Reference
- ↑ Kaiser 2004: str. 7.71–7.72.
- ↑ Nilsson & Riedel. str. 308.
- ↑ Agarwal & Lang 2005: str. 641
- ↑ Irwin 2006: str. 217–220
- ↑ Agarwal & Lang 2005: str. 646
- ↑ Nilsson & Riedel. str. 287-288.
- ↑ Irwin 2006: str. 532
- ↑ Agarwal & Lang 2005: str. 648
- ↑ 9,0 9,1 Nilsson & Riedel. str. 295.
- ↑ Humar 2002: str. 223–224 harvnb error: no target: CITEREFHumar2002 (help)
- ↑ Agarwal & Lang 2005: str. 692
- ↑ Nilsson & Riedel. str. 303.
- ↑ Irwin 2006: str. 220
- ↑ Ova sekcija je bazirana na primeru 4.2.13 od Lokenath Debnath, Dambaru Bhatta, Integral transforms and their applications, 2nd ed. Chapman & Hall/CRC. 2007. ISBN 978-1-58488-575-7. pp. 198-202 (neke notacije su promenjene kako bi odgovarale ovom članku.)
- ↑ Kumar & Kumar, Electric Circuits & Networks. str. 464.
- ↑ Nilsson & Riedel. str. 286.
- ↑ Kaiser 2004: str. 5.26–5.27.
- ↑ Agarwal & Lang 2005: str. 805
- ↑ 19,0 19,1 19,2 19,3 Cartwright, K. V.; Joseph, E.; Kaminsky, E. J. (2010). „Finding the exact maximum impedance resonant frequency of a practical parallel resonant circuit without calculus”. The Technology Interface International Journal 11 (1): 26-34. Arhivirano iz originala na datum 03. 12. 2013. Pristupljeno 29. 11. 2013.
- ↑ Kaiser 2004: str. 5.25–5.26.
- ↑ 21,0 21,1 21,2 21,3 21,4 21,5 21,6 21,7 Blanchard, Julian (1941). „The History of Electrical Resonance”. Bell System Technical Journal (USA: American Telephone & Telegraph Co.) 20 (4): 415-. DOI:10.1002/j.1538-7305.1941.tb03608.x. Arhivirano iz originala na datum 29. 07. 2013. Pristupljeno 25. 2. 2013.
- ↑ Savary, Felix (1827). „Memoirs sur l'Aimentation”. Annales de Chimie et de Physique (Paris: Masson) 34: 5-37.
- ↑ 23,0 23,1 23,2 23,3 23,4 Kimball, Arthur Lalanne (1917). A College Text-book of Physics, 2nd Ed.. New York: Henry Hold and Co.. str. 516-517.
- ↑ 24,0 24,1 24,2 Huurdeman, Anton A. (2003). The worldwide history of telecommunications. USA: Wiley-IEEE. ISBN 978-0-471-20505-0.
- ↑ Kaiser 2004: str. 7.14–7.16.
- ↑ Kaiser 2004: str. 7.21.
- ↑ 27,0 27,1 Kaiser 2004: str. 7.21–7.27.
- ↑ Kaiser 2004: str. 7.30–7.34.
Literatura
- Huurdeman, Anton A. (2003). The worldwide history of telecommunications. USA: Wiley-IEEE. str. 199-200. ISBN 978-0-471-20505-0.
- Kimball, Arthur Lalanne (1917). A College Text-book of Physics, 2nd Ed.. New York: Henry Hold and Co.. str. 516-517.
- Agarwal, Anant; Lang, Jeffrey H. (2005). Foundations of analog and digital electronic circuits. Morgan Kaufmann. ISBN 978-1-55860-735-4.
- J. L. Humar (2002). Dynamics of structures. Taylor & Francis. ISBN 978-90-5809-245-8.
- Irwin, J. David (2006). Basic engineering circuit analysis. Wiley. ISBN 978-7-302-13021-5.
- Kaiser, Kenneth L. (2004). Electromagnetic compatibility handbook. CRC Press. ISBN 978-0-8493-2087-3.
- James William Nilsson, Susan A. Riedel (2008). Electric circuits. Prentice Hall. ISBN 978-0-13-198925-2.








































































































