ベルトラン・ダルブーの定理

ベルトラン・ダルブーの定理（ベルトラン・ダルブーのていり、Bertrand-Darboux theorem）は、古典力学において2自由度の系のハミルトン–ヤコビ方程式の変数分離可能性に関する定理である。この定理によると、系が直交座標、極座標、放物線座標、楕円座標のいずれかで変数分離可能であるとき、またそのときに限り、運動量について2次の運動の積分が存在し求積可能である。

概要

ハミルトン–ヤコビ理論では、 n {\displaystyle n} 自由度の自励ハミルトン系において、ある座標変換 ( x 1 , ⋯ , x n ) → ( u 1 , ⋯ , u n ) {\displaystyle (x_{1},\cdots ,x_{n})\to (u_{1},\cdots ,u_{n})} のもとで対応するハミルトン–ヤコビ方程式の完全解を

S = ∑ i = 1 n S i ( u i ; α 1 , ⋯ , α n ) {\displaystyle S=\sum _{i=1}^{n}S_{i}(u_{i};\alpha _{1},\cdots ,\alpha _{n})}

という形に表示できるとき、この座標 ( u 1 , ⋯ , u n ) {\displaystyle (u_{1},\cdots ,u_{n})} を分離座標と呼び、求積することが可能となる[1]。ここで α i {\displaystyle \alpha _{i}} は積分定数であり、自励系では常にそのひとつとしてハミルトニアン（エネルギー）を取ることができる[2]。このような変数分離可能系は可積分系の重要なクラスをなす[3]。

ベルトラン・ダルブーの定理は、ハミルトニアンが H = 1 2 ( p x 2 + p y 2 ) + V ( x , y ) {\displaystyle H={\frac {1}{2}}(p_{x}^{2}+p_{y}^{2})+V(x,y)} という形を取る2自由度の系について、以下の3条件が同値であることを主張する[4]。

  1. ハミルトニアンと独立な、運動量について2次の運動の積分が存在する。
  2. ポテンシャル V {\displaystyle V} は方程式
    ( − 2 a x y − b ′ y − b x + c 1 ) ( ∂ 2 V ∂ y 2 − ∂ 2 V ∂ x 2 ) + 2 ( a y 2 − a x 2 + b y − b ′ x + c 2 ) ∂ 2 V ∂ x ∂ y + ( 6 a y + 3 b ) ∂ V ∂ x + ( − 6 a x − 3 b ′ ) ∂ V ∂ y = 0 {\displaystyle (-2axy-b'y-bx+c_{1})\left({\frac {\partial ^{2}V}{\partial y^{2}}}-{\frac {\partial ^{2}V}{\partial x^{2}}}\right)+2(ay^{2}-ax^{2}+by-b'x+c_{2}){\frac {\partial ^{2}V}{\partial x\partial y}}+(6ay+3b){\frac {\partial V}{\partial x}}+(-6ax-3b'){\frac {\partial V}{\partial y}}=0}
    を満足する。ここに a , b , b ′ , c 1 , c 2 {\displaystyle a,b,b',c_{1},c_{2}} はすべてはゼロでない定数である。
  3. 直交座標、極座標、放物線座標（英語版）、楕円座標のいずれかで変数分離可能である。

従ってベルトラン・ダルブーの定理は、運動量について2次の積分によって可積分系となる系は常に変数分離可能であること、そしてそのような分離座標はこれら4つのものしかないことを示している[4]。なお、変数分離可能でない可積分系も存在し、そのような系に関してはベルトラン・ダルブーの定理は有用な知見を与えない。例えば戸田格子の非自明な積分は運動量について2次ではないため、ベルトラン・ダルブーの定理は適用できない[5]。

分離座標

本節では4つの分離座標およびそれぞれの場合に変数分離可能なハミルトニアンとその積分について述べる。

直交座標

ポテンシャル V = U 1 ( x ) + U 2 ( y ) {\displaystyle V=U_{1}(x)+U_{2}(y)} の場合、直交座標により系は変数分離可能であり、ハミルトニアンと独立な運動の積分としては例えば Φ = 1 2 p x 2 + U 1 ( x ) {\displaystyle \Phi ={\frac {1}{2}}p_{x}^{2}+U_{1}(x)} が取れる[6]。

極座標

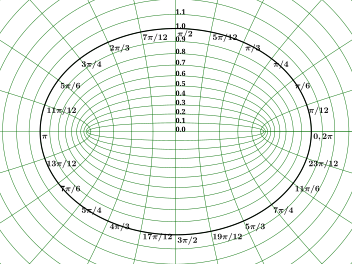
極座標 ( r , θ ) {\displaystyle (r,\theta )} は x = r cos ⁡ θ {\displaystyle x=r\cos \theta } , y = r sin ⁡ θ {\displaystyle y=r\sin \theta } により定義され、次の形のハミルトニアン

H = 1 2 ( p r 2 + p θ 2 r 2 ) + U 1 ( r ) + U 2 ( θ ) r 2 {\displaystyle H={\frac {1}{2}}\left(p_{r}^{2}+{\frac {p_{\theta }^{2}}{r^{2}}}\right)+U_{1}(r)+{\frac {U_{2}(\theta )}{r^{2}}}}

の場合に変数分離可能となる。独立な積分は

Φ = 1 2 p θ 2 + U 2 ( θ ) {\displaystyle \Phi ={\frac {1}{2}}p_{\theta }^{2}+U_{2}(\theta )}

である[7]。

放物線座標

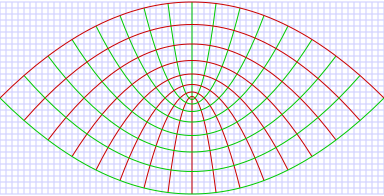
ポテンシャル V {\displaystyle V} が V = 1 r [ U 1 ( r + x 2 ) + U 2 ( r − x 2 ) ] {\displaystyle V={\frac {1}{r}}\left[U_{1}\left({\frac {r+x}{2}}\right)+U_{2}\left({\frac {r-x}{2}}\right)\right]} という形を取るとき、この系は放物線座標 ( ξ , η ) {\displaystyle (\xi ,\eta )} により変数分離可能である[8]。この座標は以下のように定義される。

{ ξ = ( r + x ) / 2 η = ( r − x ) / 2 ,     { x = ξ − η y = 2 ξ η {\displaystyle {\begin{cases}\xi =(r+x)/2\\\eta =(r-x)/2\end{cases}},\ \ {\begin{cases}x=\xi -\eta \\y=2{\sqrt {\xi \eta }}\end{cases}}}

このとき、ハミルトニアンは

H = 1 2 ξ p ξ 2 + η p η 2 ξ + η + U 1 ( ξ ) + U 2 ( η ) ξ + η {\displaystyle H={\frac {1}{2}}{\frac {\xi p_{\xi }^{2}+\eta p_{\eta }^{2}}{\xi +\eta }}+{\frac {U_{1}(\xi )+U_{2}(\eta )}{\xi +\eta }}}

という形を取り、独立な積分としては

Φ = 1 2 ξ η ( p ξ 2 − p η 2 ) ξ + η + η U 1 ( ξ ) − ξ U 2 ( η ) ξ + η {\displaystyle \Phi ={\frac {1}{2}}{\frac {\xi \eta (p_{\xi }^{2}-p_{\eta }^{2})}{\xi +\eta }}+{\frac {\eta U_{1}(\xi )-\xi U_{2}(\eta )}{\xi +\eta }}}

が取れる[9]。このような系の例としては、一様な外力場のもとでのケプラー問題がある（対応する量子系はシュタルク効果により知られている）[8]。

楕円座標

Elliptic coordinate system

x {\displaystyle x} 軸上の2点 ( ± c , 0 ) {\displaystyle (\pm c,0)} と任意の点 ( x , y ) {\displaystyle (x,y)} との距離は r 1 = ( x − c ) 2 + y 2 {\displaystyle r_{1}={\sqrt {(x-c)^{2}+y^{2}}}} および r 2 = ( x + c ) 2 + y 2 {\displaystyle r_{2}={\sqrt {(x+c)^{2}+y^{2}}}} により与えられる。このとき、ポテンシャル

V = 1 r 1 r 2 [ U 1 ( r 2 + r 1 2 ) + U 2 ( r 2 − r 1 2 ) ] {\displaystyle V={\frac {1}{r_{1}r_{2}}}\left[U_{1}\left({\frac {r_{2}+r_{1}}{2}}\right)+U_{2}\left({\frac {r_{2}-r_{1}}{2}}\right)\right]}

により記述される系は楕円座標 ( μ , ν ) {\displaystyle (\mu ,\nu )} により変数分離される[10]。その定義は

μ = r 2 + r 1 2 ,     ν = r 2 − r 1 2 {\displaystyle \mu ={\frac {r_{2}+r_{1}}{2}},\ \ \nu ={\frac {r_{2}-r_{1}}{2}}}

であり、ハミルトニアンは

H = 1 2 ( μ 2 − c 2 ) p μ 2 + ( c 2 − ν 2 ) p ν 2 μ 2 − ν 2 + U 1 ( μ ) + U 2 ( ν ) μ 2 − ν 2 , {\displaystyle H={\frac {1}{2}}{\frac {(\mu ^{2}-c^{2})p_{\mu }^{2}+(c^{2}-\nu ^{2})p_{\nu }^{2}}{\mu ^{2}-\nu ^{2}}}+{\frac {U_{1}(\mu )+U_{2}(\nu )}{\mu ^{2}-\nu ^{2}}},}

独立な積分は

Φ = 1 2 ν 2 ( μ 2 − c 2 ) p μ 2 + μ 2 ( c 2 − ν 2 ) p ν 2 μ 2 − ν 2 + ν 2 U 1 ( μ ) + μ 2 U 2 ( ν ) μ 2 − ν 2 {\displaystyle \Phi ={\frac {1}{2}}{\frac {\nu ^{2}(\mu ^{2}-c^{2})p_{\mu }^{2}+\mu ^{2}(c^{2}-\nu ^{2})p_{\nu }^{2}}{\mu ^{2}-\nu ^{2}}}+{\frac {\nu ^{2}U_{1}(\mu )+\mu ^{2}U_{2}(\nu )}{\mu ^{2}-\nu ^{2}}}}

である[11]。楕円座標を用いて積分される系としては重力2中心問題が知られている[10]。

変数分離可能性の判定

可積分かどうかわからないハミルトニアンに対してベルトラン・ダルブーの定理を適用することにより、その系が変数分離可能であれば運動の積分を求めることができる。例えば4次の同次ポテンシャル

V = 1 4 ( x 4 + y 4 ) + ϵ 2 x 2 y 2 {\displaystyle V={\frac {1}{4}}(x^{4}+y^{4})+{\frac {\epsilon }{2}}x^{2}y^{2}}

の場合、定理の条件2.から ϵ = 0 , 1 , 3 {\displaystyle \epsilon =0,1,3} のときに限って変数分離可能（従って可積分）であることが示される[12]。なお ϵ {\displaystyle \epsilon } がそれら以外の値のとき、ベルトラン・ダルブーの定理からは系は変数分離不可能であることが従うが[13]、Ziglin 解析に基づいてその場合の非可積分性が証明できる[14]。また、一般化されたエノン・ハイレス系

H = 1 2 ( p x 2 + p y 2 + ω 1 x 2 + ω 2 y 2 ) + a x 2 y − b 3 y 3 {\displaystyle H={\frac {1}{2}}(p_{x}^{2}+p_{y}^{2}+\omega _{1}x^{2}+\omega _{2}y^{2})+ax^{2}y-{\frac {b}{3}}y^{3}}

の b = − 6 a {\displaystyle b=-6a} の場合もまた同様にベルトラン・ダルブーの定理によって変数分離可能性が証明できる[15] 。

歴史

1846年にジョゼフ・リウヴィルは2次元リーマン多様体上の運動について考察し、ある座標系 ( u , v ) {\displaystyle (u,v)} においてハミルトニアンが

H = 1 2 ( p u 2 + p v 2 ) + C ( u ) + D ( v ) A ( u ) + B ( v ) {\displaystyle H={\frac {{\frac {1}{2}}(p_{u}^{2}+p_{v}^{2})+C(u)+D(v)}{A(u)+B(v)}}}

という形を取るならば、その系は求積可能であることを示した[16][17]。なお、この場合、同時に計量テンソルは

d s 2 = { A ( u ) + B ( v ) } ( d u 2 + d v 2 ) {\displaystyle ds^{2}=\{A(u)+B(v)\}(du^{2}+dv^{2})}

という形を取り、このような系をリウヴィル系として知られている[16]。

1857年にジョゼフ・ベルトランは、ハミルトニアン

H = 1 2 g i j ( q ) p i p j + V ( q ) {\displaystyle H={\frac {1}{2}}g^{ij}(\mathbf {q} )p_{i}p_{j}+V(\mathbf {q} )}

により記述される2次元系が運動量について2次の積分を持つならば、ポテンシャル V {\displaystyle V} がある一定の条件を満足することを示した[16][18]。ジャン・ガストン・ダルブーは1901年に逆にポテンシャルがベルトランが示した条件を満足するならば第一積分が存在することを証明した[19][20]。

脚注

  1. ^ 大貫&吉田, pp. 112-114.
  2. ^ 大貫&吉田, p. 113.
  3. ^ 大貫&吉田, p. 112.
  4. ^ a b 大貫&吉田, p. 121.
  5. ^ 大貫&吉田, pp. 124-125.
  6. ^ 大貫&吉田, p. 117.
  7. ^ 大貫&吉田, pp. 117-118.
  8. ^ a b 大貫&吉田, p. 118.
  9. ^ 大貫&吉田, pp. 118-119.
  10. ^ a b 大貫&吉田, p. 120.
  11. ^ 大貫&吉田, pp. 119-120.
  12. ^ 大貫&吉田, pp. 122-123.
  13. ^ 大貫&吉田, p. 123.
  14. ^ 大貫&吉田, pp. 193-194.
  15. ^ Wojciechowski, Stefan (1984). “Separability of an integrable case of the Henon-Heiles system”. Physics Letters A 100 (6): 277–278. doi:10.1016/0375-9601(84)90535-8. ISSN 03759601. 
  16. ^ a b c Smirnov, p. 3231.
  17. ^ J. Liouville, “Sur quelques cas particuliers o`u les équations de mouvement dùn point mat´eriel peuvent s’intégrer,” J. Math. Pure Appl., 11, 345–378 (1846)
  18. ^ J. M. Bertrand, “Mémoire sur quleuques-unes des forms les plus simples qui puissent présenter les intégrales des équations différentielles du mouvement d'un point matériel,” J. Math. Pure Appl., Sér. II, 2, 113–140 (1857).
  19. ^ Smirnov, p. 3232.
  20. ^ G. Darboux, “Sur un probléme de mècanique,” Arch. Néerlandaises Sci., 6, 371–376 (1901).

参考文献

  • 大貫義郎、吉田春夫『岩波講座 現代の物理学〈1〉力学』（第2刷）岩波書店、1997年。ISBN 4-00-010431-4。 
  • Smirnov, R. G. (2008). “The classical Bertrand-Darboux problem”. Journal of Mathematical Sciences 151 (4): 3230–3244. arXiv:math-ph/0604038. doi:10.1007/s10958-008-9036-0. ISSN 1072-3374. 
  • Marshall, Ian; Wojciechowski, Stefan (1988). “When is a Hamiltonian system separable?”. Journal of Mathematical Physics 29 (6): 1338–1346. doi:10.1063/1.527926. ISSN 0022-2488. 
  • Hietarinta, Jarmo (1987). “Direct methods for the search of the second invariant”. Physics Reports 147 (2): 87–154. doi:10.1016/0370-1573(87)90089-5. ISSN 03701573. 

関連項目