Cuádrica

En matemáticas, una cuádrica o superficie cuádrica es una generalización de la noción de cónica del plano a dimensiones superiores. Son superficies en el espacio o hipersuperficies (de dimensión ${\displaystyle n-1}$) en un espacio ${\displaystyle n}$-dimensional definidas como el conjunto de ceros de un polinomio irreducible de grado dos en ${\displaystyle n}$ variables, es decir, por una ecuación de la forma

${\displaystyle P(x_{1},x_{2},...,x_{n})=0}$,

donde P es un polinomio de segundo grado en las coordenadas ${\displaystyle x_{1},x_{2}...x_{n}}$. Cuando el polinomio no es absolutamente irreducible, el conjunto de ceros no se suele considerar una cuádrica, o se denomina cuádrica degenerada o cuádrica reducible.

Cuando no se precisa, es una superficie del espacio tridimensional real usual, en un sistema de coordenadas ortogonal y unitario, y las coordenadas se llaman x, y, z.

Historia

Fueron los matemáticos griegos de la antigüedad quienes iniciaron el estudio de las cuádricas, con el cono (una cuádrica) y sus secciones, que son las cónicas, curvas en un plano bidimensional, aunque no emplearon ecuaciones.

Definición algebraica

Una cuádrica afín, o superficie cuádrica afín, es una hipersuperficie n-dimensional correspondiente al conjunto de ceros de un polinomio de grado dos. Las variables del polinomio representan coordenadas en el espacio afín, de forma que el conjunto de puntos de la cuádrica es el conjunto de puntos cuyas coordenadas en una referencia afín prefijada. Si estas coordenadas son ${\displaystyle \{x_{1},x_{2},...,x_{n}\}\,}$, entonces la cuádrica típica en ese espacio se define mediante la ecuación algebraica:

${\displaystyle p(x_{1},\dots ,p_{n})=\sum _{i,j=1}^{n}Q_{i,j}x_{i}x_{j}+\sum _{i=1}^{n}P_{i}x_{i}+R=0}$

donde ${\displaystyle Q}$ es una matriz cuadrada de dimensión ${\displaystyle n\times n}$, ${\displaystyle P}$ es un vector de dimensión ${\displaystyle n}$ y ${\displaystyle R}$ es una constante. Si bien ${\displaystyle Q,P}$ y ${\displaystyle R}$ son por lo general reales o complejos, una cuádrica puede definirse en general sobre cualquier anillo.

Cuádricas del espacio euclídeo

Ecuación cartesiana

Esta sección se centra en las cuádricas del espacio euclídeo real tridimensional. La ecuación cartesiana de una superficie cuádrica de este espacio es de la forma:

${\displaystyle Ax^{2}+By^{2}+Cz^{2}+Dxy+Eyz+Fxz+Gx+Hy+Iz+J=0\,}$,

donde ${\displaystyle A,B,C,D,E,F,G,H,I,J\in \mathbb {R} }$ y al menos uno de los coeficientes ${\displaystyle A,B}$ y ${\displaystyle C}$ es no nulo.

La definición algebraica de las cuádricas incluye casos degenerados que no se corresponden con la intuición geométrica que se tiene de ellas.

Por ejemplo, la ecuación:

${\displaystyle x^{2}+y^{2}+z^{2}+2xy+2yz+2xz=0\ }$

es de segundo grado pero, también se puede escribir como:

${\displaystyle (x+y+z)^{2}=0\ }$

que equivale a:

${\displaystyle x+y+z=0\ }$,

una ecuación de primer grado que corresponde a un plano, superficie que no tiene las propiedades relacionadas con el segundo grado. Generalmente, se descartan todos los polinomios de segundo grado que son cuadrados.

• A menudo, es útil recordar que si la ecuación en su forma cartesiana carece de términos cruzados, i.e., los coeficientes D, E y F son iguales a cero:

${\displaystyle D=0,E=0,F=0}$

entonces los términos lineales para cada variable:

${\displaystyle Gx,Hy,Iz}$

pueden asimilarse a los cuadráticos:

${\displaystyle Ax^{2},By^{2},Cz^{2}}$

mediante el método de completar cuadrados, de modo que sea fácil interpretar la ecuación como una de las formas "normalizadas" que se presentan a continuación, pero "descentrada" o "trasladada" (no centrada en el origen, ${\displaystyle (0,0,0)}$, sino en un punto de coordenadas implícitas en la nueva forma).

Ecuación normalizada

La ecuación normalizada de una cuádrica tridimensional, centrada en el origen (0, 0, 0) de un espacio tridimensional, es de la forma de una de las siguientes:

${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+\varepsilon _{1}{z^{2} \over c^{2}}+\varepsilon _{2}=0,}$

${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}+\varepsilon _{3}=0,}$

${\displaystyle {x^{2} \over a^{2}}+\varepsilon _{4}=0,}$

${\displaystyle z={x^{2} \over a^{2}}+\varepsilon _{5}{y^{2} \over b^{2}},}$

donde ${\displaystyle a,b,c\in \mathbb {R} }$ y ${\displaystyle \varepsilon _{i}=0,\pm 1}$ para ${\displaystyle i=1,2,4,5}$ y ${\displaystyle \varepsilon _{3}=0,1}$.

El teorema del eje principal demuestra que, para cualquier cuádrica, existe un cambio de coordenadas cartesianas (o, equivalentemente, una transformación euclídea, es decir, que conserva las distancias) que permite que la ecuación de la cuádrica en la nueva referencia sea normalizada. Esta ecuación se llama normalizada porque dos cuádricas tienen la misma forma normalizada si y sólo si hay una transformación euclídea que transforma los puntos de una en los de la otra. Que dos cuádricas tengan la misma forma normalizada es una relación de equivalencia, lo que permite clasificarlas todas según cuál tienen, como se ve a continuación.

Clasificación afín y métrica de las cuádricas

Por medio de traslaciones y rotaciones (transformaciones euclídeas, es decir, que conservan la distancia) cualquier cuádrica se puede transformar en una que tiene su ecuación en forma normalizada, como se ha definido en el apartado anterior. En el espacio euclídeo real tridimensional una cuádrica queda pues totalmente determinada por los coeficientes de su forma normalizada.

Afínmente (es decir, ignorando la noción de distancia), las transformaciones que se pueden usar para transformar una cuádrica en otra son más amplias (no hace falta que conserven la distancia, sólo las alineaciones y razones simples) y por medio de homotecias podemos suponer que todos los coeficientes de las formas normalizadas son ${\displaystyle \pm 1}$. Se obtienen así exactamente 17 opciones, aunque sólo nueve cuádricas "verdaderas": un cono y tres cilindros (llamados habitualmente cuádricas degeneradas) y cinco cuádricas no degeneradas (elipsoides, paraboloides e hiperboloides). El resto son las cuádricas imaginarias, que constan de puntos de coordenadas complejas, (elipsoide imaginario (sin ningún punto real), cilindro imaginario (sin ningún punto real) y cono imaginario (con un único punto real)) y las cuádricas reducibles, que pueden descomponerse en dos planos. De estas últimas hay cinco tipos, dependiendo de si los planos son distintos o no, paralelos o no, y reales o complejos.

La clasificación se muestra en la siguiente tabla:

Cuádricas reales no degeneradas
Elipsoide	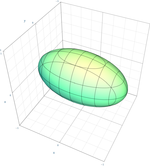${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1\,}$
Paraboloide elíptico	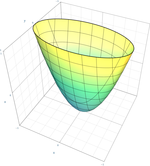${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0\,}$
Paraboloide hipérbolico	${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0\,}$
Hiperboloide de una hoja        o    hiperboloide hiperbólico	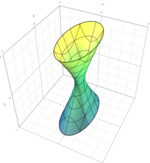${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1\,}$
Hiperboloide de dos hojas       o hiperboloide elíptico	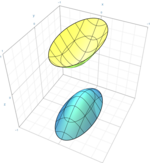${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1\,}$

Cuádricas reales degeneradas
Cono elíptico	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0\,}$
Cilindro elíptico	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,}$
Cilindro hiperbólico	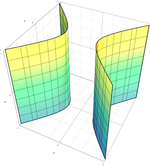${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,}$
Cilindro parabólico	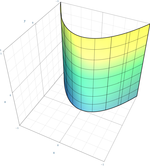${\displaystyle x^{2}+2ay=0\,}$

Con una definición más general de cuádrica (una que permite considerarlas en un espacio proyectivo general), también existe una clasificación proyectiva en el espacio proyectivo real, donde dos cuádricas son equivalentes si existe una proyectividad entre ellas (una aplicación que respeta la estructura proyectiva). Estas transformaciones son menos restrictivas y muestran que el elipsoide, el hiperboloide elíptico y el paraboloide elíptico estan de hecho relacionados, igual que los dos paraboloides hiperbólicos (por ser superficies regladas) y el cono y el cilindro (por ser cuádricas degeneradas). En el espacio proyectivo complejo todas las cuádricas no degeneradas resultan indistinguibles entre sí.

Véase también

• Cónica

Enlaces externos

• Cuádricas, en wmatem.eis.uva.es
• El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.