Zweitor
Ein Zweitor ist ein Modell für ein elektrisches Bauelement oder ein elektrisches Netzwerk mit vier Anschlüssen, bei dem je zwei Anschlüsse zu einem sogenannten Tor zusammengefasst werden. Ein Tor liegt dann vor, wenn die elektrische Stromstärke durch beide Anschlüsse eines Tors gegengleich ist, d. h. die Torbedingung erfüllt ist. Ein Zweitor ist eine spezielle Form eines allgemeinen Vierpols und andererseits ein Spezialfall eines n-Tores welches auch als Mehrtor bezeichnet wird (siehe auch: Dreitor und Viertor).
Allgemeines

Da bei einem allgemeinen Vierpol die Torbedingung nicht gelten muss, sind zu seiner Beschreibung drei Gleichungen mit drei Strom- und drei Spannungsvariablen notwendig. Bei nachfolgend ausschließlich behandelten Zweitoren, d. h. bei Vierpolen mit gültigen Torbedingungen und bei Dreipolen (z. B. Transistoren) werden dagegen nur zwei Gleichungen mit zwei Strom- und zwei Spannungsvariablen benötigt.[1]
Aus historischen Gründen werden vor allem in der älteren Fachliteratur die Begriffe „Zweitor“ und „Vierpol“ synonym verwendet, d. h. unter dem Begriff „Vierpol“ (im engeren Sinne) wird implizit immer ein Zweitor verstanden. Ebenso werden die Bezeichnungen Zweitortheorie und Vierpoltheorie sowie Torbedingungen und Vierpolbedingungen gleichbedeutend benutzt.
Insbesondere bei den sogenannten Übertragungsvierpolen, die sich zwischen einem Generator- und einem Lastzweipol befinden und zur Übertragung und/oder Verarbeitung von analogen Signalen oder elektrischer Energie dienen, werden die Tore auch als Eingang und als Ausgang bezeichnet.
Zweitortheorie
Unter Zweitortheorie versteht man ein Teilgebiet der Elektrotechnik, das sich als ein Verfahren zur Analyse elektrischer Netzwerke mit der Verhaltensbeschreibung und Berechnung von linearen zeitinvarianten Zweitoren beschäftigt. Einerseits beschreibt sie die Zweitore nur durch ihre Zweitorparameter als Blackbox, andererseits stellt sie Ersatzschaltbilder und Verfahren zur Ermittlung des Verhaltens von zusammengesetzten Zweitoren bereit. Während sich die „klassische Vierpoltheorie“ im Wesentlichen mit der Analyse von passiven umkehrbaren Zweitoren beschäftigte, wurden mit Beginn der Analogelektronik auch aktive nichtumkehrbare Zweitore im Rahmen der Kleinsignaltheorie für Elektronenröhren, Transistoren und Operationsverstärker zum Gegenstand der „modernen Zweitortheorie“.
Die Zweitortheorie ist die Basis der Filtertheorie und -technik. Die Struktursynthese von Zweitoren („Vierpolsynthese“) ist nicht Gegenstand der Zweitortheorie, baut aber natürlicherweise auf ihren Erkenntnissen auf. Eine Verallgemeinerung der Zweitortheorie ist die n-Tor-Theorie (auch als Mehrtortheorie bezeichnet). Diese lässt beliebig viele Tore zu, unterscheidet nicht zwischen Ein- und Ausgangstoren und nutzt zur Beschreibung hauptsächlich Streuparameter. Die Methoden der Zweitortheorie können auf elektromechanische und nichtelektrische Systeme verallgemeinert werden. Beispielsweise wird eine ideale Gleichstrommaschine als Zweitor betrachtet, deren Eingang durch Spannung und Strom, ihr Ausgang jedoch durch Drehzahl und Drehmoment beschrieben werden.
Die Wurzeln der Zweitortheorie legte 1886 Oliver Heaviside mit der Theorie der homogenen Leitung, die damit ein erster Repräsentant eines Zweitors war. 1900 gab Mihajlo Pupin mit seiner Leitungsbespulung den Anstoß zu einer „Theorie der Kettenleiter“. George Ashley Campbell beschrieb 1903 einen Tiefpass als Filter und J. L. La Cour nutzte Kettengleichungen und Kettenparameter. 1915 begründete Karl Willy Wagner die Theorie der Kettenleiter und der allgemeinen Siebketten. Schließlich prägte 1921 Franz Breisig den Begriff „Vierpol“. Er baute in den 1920er Jahren mit Julius Wallot die Vierpoltheorie zu einer selbständigen Theorie aus. Felix Strecker und Richard Feldtkeller schlossen 1929 die „Allgemeine Vierpoltheorie“ durch Einführung der Matrizenrechnung ab. Die Verallgemeinerung der Erkenntnisse der klassischen Vierpoltheorie war gleichzeitig der Ausgangspunkt der Ausarbeitung einer Theorie linearer Systeme.[2]
Zweitorgleichungen
Das Klemmenverhalten eines Zweitors wird durch zwei Zweitorgleichungen beschrieben, welche zwei Klemmenstromvariablen ( und ) und zwei Klemmenspannungsvariablen ( und ) zueinander in Beziehung setzen. Bei diesem Gleichungssystem kann es sich im Allgemeinen um implizite nichtlineare Differentialgleichungen handeln. Für eine handhabbare Theorie reduziert man ihre Komplexität auf zwei algebraische Gleichungen, indem man entweder nur resistive oder nur lineare Zweitore betrachtet.
Zählpfeilsysteme
Um das Verhalten eines Zweitors eindeutig zu beschreiben, müssen die Richtungen der Zählpfeile für die beiden Spannungen und die beiden Ströme definiert werden. Während für die Spannungen die „natürliche Richtung“ (von oben nach unten) üblich ist, gibt es für die Ströme unterschiedliche Annahmen. Insbesondere wird die Pfeilrichtung des Ausgangsstromes verschieden festgelegt. In der Theorie, Literatur und Praxis existieren deshalb folgende Zählpfeilsysteme, deren Festlegungen sich in allen Zweitorgleichungen auf die Vorzeichen auswirken:
- In der klassischen Theorie der Übertragungsvierpole wird das sogenannte Kettenpfeilsystem benutzt, bei dem der Strompfeil von (anders als hier im Bild gezeigt) vom Zweitor weg zeigt. Deshalb kann die Kettenschaltung von Zweitoren durch eine einfache Matrizenmultiplikation berechnet werden.
- Dagegen wird bei Anwendung der Zweitortheorie in der elektronischen Schaltungstechnik heute meist das symmetrische Zählpfeilsystem verwendet. In diesem sind die Ströme zum Zweitor hin positiv definiert (siehe Bild). Damit lässt sich jedoch die Kettenschaltung von Zweitoren nur „umständlich“ berechnen.[3]
- Aus diesen Gründen werden oft – wie auch in diesem Artikel – beide Zählpfeilsysteme zu einem gemischten Zählpfeilsystem kombiniert. Für die Widerstands-, Leitwert und Hybridformen verwendet man das symmetrische Pfeilsystem, für die beiden Kettenformen dagegen das Kettenpfeilsystem. Das wird für diese beiden Formen durch ein negatives Vorzeichen von in der unten aufgeführten Definitionstabelle der Zweitorparameter realisiert.
Beim Studium der Literatur zur Zweitor- bzw. Vierpoltheorie muss unbedingt die vom Autor zugrunde gelegte Variante ermittelt werden, um überhaupt Vergleiche der präsentierten Formeln durchführen zu können.[4]
Die Gleichungen resistiver nichtlinearer Zweitore
Resistive Zweitore besitzen per Definition keine Blindwiderstände. Deshalb sind für ihre Verhaltensbeschreibung nichtlineare algebraische Gleichungen ausreichend. In vielen praktischen Anwendungsfällen werden diese als Kennlinienfelder dargestellt.
Ein typischer Fall ist das Großsignalverhalten eines Bipolartransistors bei niedrigen Frequenzen. Dieser kann beispielsweise durch sein nichtlineares Hybrid-Kennlinienfeld als Zweitor charakterisiert werden. Die Zweitorgleichungen nehmen dann die Form zweier nichtlinearer Funktionen und an:
Besitzt ein resistives nichtlineares Zweitor im Arbeitspunkt stetige Kennlinien, dann können diese dort linearisiert werden. In diesem Fall wird das lineare Kleinsignalverhalten des Zweitors durch zwei lineare Zweitorgleichungen mit vier das Zweitor beschreibenden Zweitorparametern (in der Literatur auch Zweitorkoeffizienten oder Zweitorkonstanten[5] genannt) beschrieben.
Beispielsweise kann das Kleinsignalverhalten des o. g. Transistors in folgender Weise ausgedrückt werden (üblicherweise wechselt man dann von der Kleinschreibung der Signalbezeichner zur Großschreibung):
Aufgrund der „vermischten“ Anordnung der Variablen bezeichnet man die Zweitorparameter , , und in diesem Beispiel als Hybridparameter.[1]
Die Gleichungen linearer Zweitore
Für lineare Zweitore mit internen Blindwiderständen gehen die Differentialgleichungen unter Anwendung der symbolischen Methode der Wechselstromrechnung, der Laplacetransformation oder einer anderen Operatorenrechnung ebenfalls in ein Paar lineare algebraische Gleichungen über. Die vier das Zweitor beschreibenden Zweitorparameter sind damit im Allgemeinen von der (evtl. komplexen) Kreisfrequenz abhängige Operatoren, also Übertragungsfunktionen bzw. Frequenzgänge im Sinne der Theorie linearer Systeme.
Durch die Möglichkeiten bei der konkreten Auswahl der zwei abhängigen und der zwei unabhängigen Variablen für die explizite Schreibweise des Gleichungssystems gibt es genau sechs verschiedene Formen der Zweitorgleichungen. Jede Form ist jeweils für die Berechnung einer bestimmten Zusammenschaltung von Zweitoren besonders geeignet und erhält dadurch ihre Bezeichnung. Die oben genannte Hybridform heißt deshalb auch Reihen-Parallel-Form.
Unter der Voraussetzung der Existenz der jeweiligen Parameter lassen sich die beiden linearen Zweitorgleichungen vorteilhaft, aber nicht notwendigerweise, in Form von Matrizen schreiben. Für das oben genannte Beispiel erhält man
Die Matrix
heißt dann Hybridmatrix oder Reihen-Parallel-Matrix, denn für eine eingangsseitige Reihen- und ausgangsseitige Parallelschaltung zweier Zweitore brauchen ihr Hybridmatrizen nur addiert werden.
Bei Zweitoren mit unabhängigen (ungesteuerten) Quellen[4] werden eingeprägte Ströme und Spannungen zu diesen Gleichungen als Konstanten oder in Matrizenschreibweise als Konstanten-Vektor hinzu addiert. Beispielsweise hätten dann die Hybridgleichungen folgende Form:
Eigenschaften
Zweitore lassen sich anhand ihres Klemmenverhaltens, d. h. als Blackbox, oder aufgrund ihrer inneren Struktur wie folgt klassifizieren:
Linearität
Die Übertragungsfaktoren von linearen Zweitoren sind unabhängig von Spannung und Strom. Deshalb gilt für die Torströme und -spannungen der Überlagerungssatz. Ein Zweitor, das nur aus den passiven linearen Bauelementen Widerstand, Spule, Kondensator und Übertrager besteht (ein sogenanntes RLCM-Zweitor), ist immer selbst linear.
Nichtlineare Zweitore sind Netzwerke mit mindestens einem nichtlinearen Bauelement und diese Bauelemente selbst, etwa Dioden oder Transistoren. Ihr Übertragungsverhalten hängt wesentlich von der Größe der Torströme und -spannungen ab. Eine annähernd lineare Beschreibung ist mittels der Kleinsignaltheorie bei stetigen Kennlinien und für kleine Amplituden möglich.
Nur lineare Zweitore sind Gegenstand der klassischen Vierpol- und der modernen Mehrtortheorie. Nur für sie gelten die linearen Zweitorgleichungen und damit die im Folgenden beschriebene Matrizendarstellung der Zweitorparameter.
Leistungsbilanz
Enthält ein Zweitor keine inneren ungesteuerten oder gesteuerten Energiequellen, so nennt man es passiv (z. B. Dämpfungsglied), anderenfalls aktiv. Daraus ergibt sich, dass die Ausgangswirkleistung P2 kleiner als die Eingangswirkleistung P1 sein muss. Aktive Vierpole, etwa Verstärker, entnehmen Energie aus Hilfsenergiequellen (Stromquelle).
Geht in einem (passiven) Zweitor keine Energie verloren, weil es nur Blindschaltelemente enthält, so nennt man es Reaktanzzweitor.
Symmetrieverhalten linearer Zweitore
In Bezug auf symmetrisches Verhalten von Zweitoren unterscheidet man (mit steigender Symmetrie) rückwirkungsfreie, nichtumkehrbare, umkehrbare und symmetrische Zweitore. Die entsprechenden Einschränkungen verringern die Anzahl der benötigten Zweitorparameter und beeinflussen die Form des Ersatzschaltbildes.
Umkehrbarkeit
Umkehrbare Zweitore (auch reziprok, kopplungssymmetrisch oder übertragungssymmetrisch genannt) haben in beide Richtungen dasselbe Übertragungsverhalten, d. h. beispielsweise, dass sich das Verhältnis von Ausgangsstrom und Eingangsspannung bei kurzgeschlossenem Ausgang beim Vertauschen von Eingangs- und Ausgangsklemmenpaar nicht ändert. Diese Eigenschaft wird auch als Reziprozitätstheorem oder als Kirchhoffscher Umkehrungssatz bezeichnet. Somit erzeugt eine an Tor 1 angelegte Spannung am kurzgeschlossenen Tor 2 einen Strom . Wird dieselbe Spannung an Tor 2 mit angelegt, wird derselbe Strom am kurzgeschlossenen Tor 1 erzeugt. Daraus ergibt sich wenn ist.
Reziproke Zweitore sind durch drei Zweitorparameter vollständig charakterisiert, denn für diese gelten dann folgende Einschränkungen:
Alle Zweitore, die nur aus den passiven linearen Bauelementen Widerstand, Spule, Kondensator und Übertrager bestehen (RLCM-Zweitore), sind umkehrbar. Das gilt auch für (lineare) elektrische Leitungen und Antennensysteme.
Widerstandssymmetrie
Widerstandssymmetrische Zweitore (auch impedanzsymmetrisch oder richtungssymmetrisch) haben in Vor- oder Rückwärtsrichtung bei gleicher äußerer Beschaltung die gleichen Eingangs- bzw. Ausgangsinnenwiderstände. Sie sind durch drei Zweitorparameter vollständig charakterisiert, denn für die Parameter der Zweitorgleichungen gelten folgende Einschränkungen:
Widerstandssymmetrische Zweitore müssen definitionsgemäß nicht reziprok sein.[4]
Symmetrie
Bei symmetrischen Zweitoren (im engeren Sinn) sind Ein- und Ausgang miteinander vertauschbar. Wenn das auf ein Zweitor nicht zutrifft, so wird dieses als unsymmetrisch bezeichnet. Symmetrische Zweitore sind sowohl widerstandssymmetrisch als auch umkehrbar. Deshalb gilt für die Zweitorparameter:
Symmetrische Zweitore sind somit schon durch zwei Zweitorparameter vollständig charakterisiert. Sie sind (per Definition) immer reziprok, jedoch sind reziproke Zweitore nicht immer symmetrisch. Obwohl die Ersatzschaltung von symmetrischen Zweitoren eine längssymmetrische Struktur besitzt, muss das im Allgemeinen auf ihre innere Struktur nicht zutreffen.
Rückwirkungsfreiheit
Hat eine sich (durch Belastung) verändernde Ausgangsgröße keinen Einfluss auf die Eingangsgrößen, so nennt man das Zweitor rückwirkungsfrei. Rückwirkungsfreie Zweitore sind ein „Extremfall“ nichtumkehrbarer Zweitore. Für die Parameter eines rückwirkungsfreien Zweitors gelten folgende Einschränkungen:
Damit sind die Eingangsgrößen , von den Ausgangsgrößen , unabhängig. Der Idealfall eines rückwirkungsfreien Zweitors ist die gesteuerte Quelle.
Strukturelle Eigenschaften von zusammengesetzten Zweitoren
Aufbausymmetrie
Bei längssymmetrischen Zweitoren kann in Querrichtung eine Symmetrielinie eingezeichnet werden. Längssymmetrische Zweitore sind immer auch symmetrisch (im engeren Sinne) und können mit besonderen Methoden analysiert werden.
Bei quersymmetrischen oder erdungssymmetrischen Zweitoren kann in Längsrichtung eine Symmetrielinie eingezeichnet werden. Das bedeutet, dass keine durchgehende Erdleitung vorhanden ist. Ein typisches Beispiel ist die sogenannte X-Schaltung. Die in der Praxis als Zweitor verwendeten Dreipole haben dagegen eine durchgehende Erdleitung und sind deshalb erdungsunsymmetrisch. Die Eigenschaft der Erdungssymmetrie hat keinen Einfluss auf die Zweitorparameter. Theoretisch kann man mit Hilfe von idealen Übertragern erdungssymmetrische Zweitore in erdungsunsymmetrische und umgekehrt verwandeln.
RLCM-Zweitore
Zweitore, welche nur aus den linearen Bauelementen Widerstand (R), Spule (L), Kondensator (C) und Übertrager (M) bestehen, nennt man in der Literatur RLCM-Zweitore. Sie sind immer umkehrbar und passiv. Enthalten sie keine ohmschen Widerstände, dann sind sie verlustlos und heißen Reaktanzzweitore. Enthalten sie ausschließlich ohmsche Widerstände, dann nennt man sie resistive Zweitore. Diese sind immer verlustbehaftet passiv und können z. B. als Dämpfungsglied benutzt werden.
Zweitorparameter
Definition der Parameter von linearen Zweitoren

Insgesamt gibt es verschiedene Zweitorparameter, deren Bedeutung aus den Definitionsgleichungen in der folgenden Tabelle zu erkennen ist. Sie werden jeweils bei Kurzschluss oder Leerlauf an einem Tor berechnet (sofern die innere Struktur des Zweitors bekannt ist) oder gemessen (sofern das Zweitor „real existiert“). Dabei handelt es sich um 8 Eingangs- oder Ausgangs-Impedanzen bzw. −Admittanzen, 8 Spannungs- oder Stromübersetzungen in Vor- oder Rückwärtsrichtung und 8 sogenannte Kern-Impedanzen oder −Admittanzen in Vor- oder Rückwärtsrichtung.
Die Definitionen aller Zweitorparameter sind in der folgenden Tabelle in Form von Matrizengleichungen aufgeführt.
| Z-Charakteristik | : Impedanzmatrix, existent, falls die Torströme (I1 und I2) unabhängig wählbar sind. : Leerlauf-Eingangsimpedanz | |
| Y-Charakteristik | : Admittanzmatrix, existent, falls die Torspannungen (U1 und U2) unabhängig wählbar sind. : Kurzschluss-Eingangsadmittanz | |
| H-Charakteristik | : Hybridmatrix (Reihen-Parallel-Matrix), existent, falls I1 und U2 unabhängig wählbar sind. : Kurzschluss-Eingangsimpedanz | |
| P-Charakteristik | : Inverse Hybridmatrix (Parallel-Reihen-Matrix), existent, falls U1 und I2 unabhängig wählbar sind. : Leerlauf-Eingangsadmittanz | |
| A-Charakteristik | : Kettenmatrix : Reziproke Leerlauf-Spannungsübersetzung | |
| B-Charakteristik | : Inverse Kettenmatrix : Reziproke Leerlauf-Spannungsrückwirkung |
Hinweis: Statt des Symbols werden auch oder und statt des Symbols wird auch verwendet.
Umrechnung der Matrizen
Wie die folgende Umrechnungstabelle zeigt, gelten im Fall der Existenz der Matrizen insbesondere folgende Beziehungen:
Umrechnung der Determinanten
Zusammenschaltung von Zweitoren
Zwei Zweitore können unter der Voraussetzung, dass die oben genannte Torbedingung an mindestens einem Tor erfüllt wird, zu einem neuen Zweitor zusammengeschaltet werden. Zur Überprüfung der Zulässigkeit der Zusammenschaltung dient der Brune-Test. Die Parameter des neu entstandenen Zweitors lassen sich aus den Parametern der beiden verschalteten Zweitore errechnen. Für jede Verschaltungsart gibt es eine Matrizendarstellung, mit der sich die Gesamtmatrix der Verschaltung besonders gut berechnen lässt. Insgesamt existieren fünf verschiedene Kombinationsmöglichkeiten von zwei Zweitoren:
| Kombination | Blockstruktur | Matrizenoperation |
|---|---|---|
| Reihenschaltung | 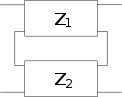 | |
| Parallelschaltung |  | |
| Hybridschaltung oder Reihen-Parallelschaltung | 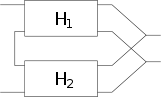 | |
| inverse Hybridschaltung oder Parallel-Reihenschaltung | 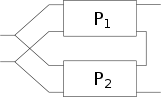 | bzw. bzw. |
| Kettenschaltung |  | oder bzw. |
Vertauschen von Zweitoren

Oftmals ist es hilfreich ein Zweitor durch ein Anderes hindurch zu transformieren. Dafür seien die Zweitore A und T in Kettenparametern gegeben, T sei außerdem invertierbar und soll nicht verändert werden. Bei der Verschiebung durch T hindurch wird A nun zu A', sodass sich das Verhalten des Gesamtzweitors nicht ändert. Demzufolge muss gelten:
Eine besondere Rolle spielen hier die transformatorische Kopplung wo nur die Hauptdiagonale von T ist besetzt und die gyratorische Kopplung wo die Hauptdiagonale von T Null ist. Einfache Impedanzen können durch die nebenstehenden Matrizen in Kettenparametern ausgedrückt werden. Im Falle transformatorischer oder gyratorischer Kopplung sind dann A und A' von der Form her eine dieser beiden Matrizen, sprich eine einzelne Impedanz Z auf einer Seite von T kann durch eine einzelne Impedanz Z' auf der anderen Seite ausgedrückt werden. Bei der gyratorischen Kopplung werden dabei Parallel- zu Reihenschaltungen und umgekehrt. Auf diese Weise ist es möglich, ganze Netzwerke durch ein Zweitor hindurch zu projizieren.
Elementar-Zweitore

Elementar-Längszweitor
Das Elementar-Längszweitor enthält lediglich einen Zweipol mit der Impedanz in der oberen Längsachse zwischen den oberen Polen des Zweitors. Es gibt keine Verbindung zwischen den Polen in der Querachse.
Elementar-Querzweitor
Das Elementar-Querzweitor enthält lediglich einen Zweipol mit der Admittanz in der Querachse des Zweitors, aber keine Elemente in der Längsachse.
Γ-Zweitor
Das Γ-Zweitor ist eine Kettenschaltung aus Elementar-Querzweitor und Elementar-Längszweitor. Seine Kettenmatrix bildet sich aus den Kettenmatrizen der Elementar-Zweitore durch Matrizenmultiplikation wie folgt:
Gespiegeltes Γ-Zweitor
Das gespiegelte Γ-Zweitor ist eine Kettenschaltung aus Elementar-Längszweitor und Elementar-Querzweitor. Seine Kettenmatrix bildet sich aus den Kettenmatrizen der Elementar-Zweitore wie folgt:
Ideale Zweitore
Ein ideales Zweitor dient als fiktives Bauelement in der Netzwerktheorie und in Ersatzschaltungen, kann aber bei Bedarf (meist nur mit Hilfe von realen aktiven Bauelementen) angenähert nachgebildet werden. Ideale Zweitore lassen sich nach der „Besetzung“ ihrer Kettenmatrix klassifizieren:
- Beim Nullor sind alle Elemente der Kettenmatrix 0. Er ist das Modell eines idealen Operationsverstärkers mit unendlicher Verstärkung.
- Bei einer gesteuerten Quelle ist genau ein Element der Kettenmatrix ungleich 0. Deshalb gibt es vier sich unterschiedlich verhaltende Varianten. Gesteuerte Quellen modellieren ideale rückwirkungsfreie Verstärker und werden unbedingt in Ersatzschaltbildern von realen aktiven oder/und nichtumkehrbaren Zweitoren benötigt.
- Bei einem Impedanzkonverter sind nur die Elemente der Hauptdiagonale der Kettenmatrix ungleich 0. Er kann eine an seinem Ausgang angeschlossene Impedanz durch Multiplikation mit einem Konversionsfaktor in eine quantitativ und qualitativ andere Impedanz an seinem Eingang „umwandeln“. Wichtige Spezialfälle sind der Negativimpedanzkonverter (NIC) und der ideale Übertrager. Letzterer beinhaltet beim Übersetzungsverhältnis von +1 oder −1 außerdem die durchgehende bzw. gekreuzte Verbindung als Zweitor.
- Beim Impedanzinverter sind dagegen nur die Elemente der Nebendiagonale der Kettenmatrix ungleich 0. Er kann eine an seinem Ausgang angeschlossene Impedanz in ihre duale Impedanz durch Kehrwertbildung (Inversion) wandeln. Der praktisch wichtigste Anwendungsfall ist der Gyrator, welcher beispielsweise aus einer Kapazität eine Induktivität machen kann.
Ersatzschaltungen
Zur Vereinfachung von Rechnungen können komplexe Zweitore mithilfe entsprechender Zweitorparameter zu vereinfachten Schaltungen zusammengefasst werden. Die Ersatzschaltungen stellen keine Anleitung zur physikalischen Realisierung dar.
T-Ersatzschaltung

Die T-Ersatzschaltung ermöglicht die Darstellung eines beliebigen Zweitors mithilfe der Ersatzimpedanzen. Bei umkehrbaren Zweitoren entfällt die gesteuerte Spannungsquelle. Es kann aus einem Elementar-Längszweitor und einem Γ-Zweitor oder entsprechend aus einem gespiegelten Γ-Zweitor und einem Elementar-Längszweitor synthetisiert werden. Nachfolgende Zusammensetzung beschreibt letzteres:
π-Ersatzschaltung

Die π-Ersatzschaltung ermöglicht die Darstellung eines beliebigen Zweitors mithilfe der Ersatzadmittanzen. Bei umkehrbaren Zweitoren entfällt die gesteuerte Stromquelle. Es kann aus einem Elementar-Querzweitor und einem gespiegelten Γ-Zweitor oder entsprechend aus einem Elementar-Querzweitor und einem Γ-Zweitor synthetisiert werden. Nachfolgende Zusammensetzung beschreibt letzteres:
Weitere Zweitorparameter
Neben der Charakterisierung eines Zweitors durch die oben beschriebenen Zweitorparameter gibt es für besondere Anwendungszwecke auch andere Darstellungsformen. So kann ein lineares Zweitor auch durch sogenannte Streuparameter beschrieben werden. Diese Darstellungsform ist vor allem im Bereich der Hochfrequenztechnik üblich, da dabei die Anschlüsse des Zweitors nicht kurzgeschlossen bzw. leerlaufen müssen, sondern im Regelfall durch ihre Wellenimpedanz abgeschlossen sind.
Zwischen den S-Parametern und den oben erwähnten Y-Parametern der Admittanzmatrix eines Zweitors besteht mit der Wellenimpedanz ZW folgender Zusammenhang:
mit der Abkürzung:
Symmetrische lineare Zweitore werden für ihre Anwendung in der Theorie der Siebschaltungen (Wellenparametertheorie) durch die sogenannten Wellenparameter beschrieben. Die zwei das Zweitor beschreibenden Parameter sind dabei die Wellenimpedanz und das Wellenübertragungsmaß.
Numerische CAD-Systeme in der Elektronik
Die praktische Auswertung und Verarbeitung obiger Matrizen aus komplexen Elementen erfordert den Einsatz von Rechnern. Seit den 1970er-Jahren wird von der rechnergestützten numerischen Auswertung und Weiterverarbeitung obiger Gleichungen berichtet, und ab den 1980er-Jahren setzten sich dann aufwendige numerische CAD-Systeme (z. B. Super-Compact) schrittweise in der Industrie durch. Dabei besteht kein grundsätzlicher Unterschied zwischen der Hochfrequenz- und Mikrowellenelektronik und der Elektronik bei tieferen Frequenzen. Die linearen Abhängigkeiten zwischen Strom und Spannung wird bei allen Frequenzen durch die obigen sechs Vierpolformen und völlig gleichwertig durch s- und t-Parameter (eine s-Parameter-Kettenform) beschrieben, solange überhaupt die Begriffe von Strom und Spannung als „Ersatzgrößen“ anstelle der elektromagnetischen Felder und anderer physikalischer Begriffe genommen werden können. In vielen Fällen ist dies bis in den Mikrowellenbereich möglich, ohne dass mit erheblich mehr Rechenaufwand vollnumerisch die Feldgleichungen für die elektromagnetischen Felder zu lösen wären. Der Übergang ist dabei aber stets fließend.
Symbolische CAD-Systeme für rechnergestützte Formelherleitungen
Von Interesse ist weiterhin auch die symbolische Verarbeitung obiger Matrizengleichungen und darauf aufbauend die rechnergestützte Formelherleitung für die Signalanalyse in der linearen Elektronik und Hochfrequenzelektronik. Ein spezieller Zusatz[6] für ein Mathematikprogramm wandelt dabei die obigen acht Vierpolparameterdarstellungen zuzüglich der Wellenparameterform und ergänzt durch zahlreiche weitere Modelle (aktive Elemente wie Einzeltransistoren und Standardschaltungen sowie passive Elemente wie Leitung, Transformator, Koppler, Richtungsleitung: alle mit ihren jeweiligen Modellparametern) symbolisch und – so weit dies logisch möglich ist – von jeder Art in jede andere Art um. Die obige Vernetzung von Vierpolen wird dabei weitgehend automatisiert und durch weitere Befehle ergänzt wie z. B. das Deembedden eines eingebetteten Vierpols, das obige Durchschieben eines Vierpols durch einen anderen Vierpol hindurch, verschiedene Anschlussklemmenvertauschungen et cetera. Als Ergebnis erhält man dann von den Modellparametern und/oder den Vierpolparametern abhängige Formeln für die üblichen Reportgrößen, die bei den numerischen CAD-Systemen nur als Zahlen erscheinen: Formelsätze für Spannungs- und Stromverstärkung, Eingangs- und Ausgangsimpedanzen, Reflexionsfaktoren, Gewinngrößen oder Stabilitätsfaktor bis hin zu den verallgemeinerten Streuparametern nach Kurokawa, also für Größen, die in den numerischen Systemen Standard sind. Ein solches System ist faszinierend und eignet sich auch sehr, um neue Zusammenhänge zu erarbeiten, Ideen zu entwickeln oder Vermutungen zu beweisen bzw. zu widerlegen.
Möglichkeiten und Grenzen der CAD-Systeme
Trotz der enormen Möglichkeiten bleiben diese symbolischen ebenso wie die numerischen CAD-Systeme immer nur Rechenassistenten, die stets mit viel Sachverstand geführt werden müssen, denn sie bestehen aus mathematischen Theorien, Modellen und vielen Programmzeilen. Die Qualität aller Rechenergebnisse steht und fällt dabei immer mit der Messung.
Literatur
- Lorenz-Peter Schmidt, Gerd Schaller, Siegfried Martius: Grundlagen der Elektrotechnik. Band 3: Netzwerke. Pearson Studium, München 2006, ISBN 3-8273-7107-4.
- Richard Feldtkeller: Einführung in die Vierpoltheorie der elektrischen Nachrichtentechnik. Hirzel, Stuttgart 1976, ISBN 3-7776-0319-8.
- Handwörterbuch des elektrischen Fernmeldewesens. Aufsatz zur Vierpoltheorie von Zuhrt / Matthes, 2. Auflage. 3. Band, S. 1837–1868.
- Wolfgang Kretz: Formelsammlung zur Vierpoltheorie (mit einer kurzen Einführung). Oldenbourg, München 1967.
- Eugen Philippow: Grundlagen der Elektrotechnik. Akademische Verlagsgesellschaft Geest & Portig, Leipzig 1966.
- Heinrich Schröder: Elektrische Nachrichtentechnik. Band I, Verlag für Radio-Foto-Kinotechnik, Berlin-Borsigwalde 1966.
- Claus-Christian Timmermann: Hochfrequenzelektronik mit CAD, Bd. 1, Einführung in Leitungen, Vierpole, Transistormodelle und Simulation mit numerischen und symbolischen CAD-Systemen, Bd. 1, PROFUND-Verlag, 1997 und 2005, ISBN 978-3-932651-21-2
- George D. Vendelin, Anthony M. Pavio, Ulrich L. Rohde. Microwave Circuit Design Using Linear and Nonlinear Techniques, 2nd Edition, Wiley, 2005, ISBN 978-0-471-41479-7
- Vorlesung – Netzwerke 3. Institut für Grundlagen und Theorie der Elektrotechnik, Technische Universität Graz (Diese Thematik wird als Mehrtortheorie bezeichnet. Unter diesem Titel sollten daher weitere Quellen auffindbar sein).
- Vorlesung – Dynamische Netzwerke. Institut für Grundlagen der Elektrotechnik und Elektronik, Technische Universität Dresden
Weblinks
- Ronny Harbich: Passive Zweitore. 2005, abgerufen am 18. Januar 2010.
Einzelnachweise
- ↑ a b Klaus Lunze: Theorie der Wechselstromschaltungen. 8. Auflage. Verlag Technik GmbH, Berlin 1991, ISBN 3-341-00984-1.
- ↑ Gerhard Wunsch: Geschichte der Systemtheorie – Dynamische Systeme und Prozesse. R. Oldenbourg Verlag, München 1985, ISBN 3-486-29531-4.
- ↑ Hans Frühauf: Elektronische Bauelemente und ihre Schaltungen. 6. Lehrbrief. Verlag Technik, Berlin 1968, DNB 365178616.
- ↑ a b c Reinhold Paul: Elektrotechnik 2 – Netzwerke. Springer-Verlag, Berlin Heidelberg New York 1994, ISBN 3-540-55866-7.
- ↑ Eugen Philippow: Grundlagen der Elektrotechnik. Akademische Verlagsgesellschaft Geest&Portig K.-G., Leipzig 1967, DNB 457803371.
- ↑ Claus-Christian Timmermann, Hochfrequenzelektronik mit CAD, Bd. 1, Einführung in Leitungen, Vierpole, Transistormodelle und Simulation mit numerischen und symbolischen CAD-Systemen, Bd. 1, Anhang STWOP: Symbolische 2-Tor-Analyse, Anhang TWOP: Numerische 2-Tor-Analyse. , S.117–126

















































































































































































