Quadratwurzel aus 3

Die Quadratwurzel aus 3 oder Quadratwurzel von 3 (geschrieben ) ist die positive, reelle Zahl, die mit sich selbst multipliziert 3 ergibt. Die Wurzel von 3 ist eine irrationale Zahl. Sie ist eine mathematische Konstante, auch bekannt unter dem Namen Theodorus-Konstante, benannt nach Theodoros von Kyrene.
Näherungsweise gilt:
Ihre Kettenbruchentwicklung ist [1;1,2,1,2,1,2,1,2,1,2,…].
Es ist auch und
Beweis der Irrationalität
Angenommen, wäre rational. Dann könnte man die Zahl als Bruch zweier teilerfremder ganzer Zahlen und schreiben:
- .
Durch Quadrieren der Gleichung erhält man
daraus folgt
Aber dann ist für eine ganze Zahl
weil eine ganze Zahl ist und damit eine ganze Zahl sein muss und damit auch 3 als Teiler von existieren muss.
Daraus folgt wieder
- ,
also
Aber dann ist auch für eine ganze Zahl
- ,
was einen Widerspruch bedeutet, weil und teilerfremd sind.
Nachkommastellen
Die ersten 100 Nachkommastellen:
1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 1690880003 7081146186 7572485756[1]
Weitere Dezimalstellen finden sich auch unter Folge A002194 in OEIS.
Der derzeitige Weltrekord der Berechnung der Nachkommastellen (vom 9. Juni 2019) liegt bei 2.000.000.000.000 und wurde von Hiroyuki Oodaira (大平 寛之) erzielt.[2]
Anwendung


- Ein rechtwinkliges Dreieck mit einer kleinen Kathete gleich und einer Hypotenuse gleich hat, nach dem Satz des Pythagoras, eine große Kathete gleich .
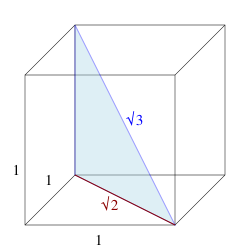
- Das Verhältnis zwischen der Diagonale eines dreidimensionalen Würfels und der Kantenlänge beträgt
- Die Distanz zwischen zwei gegenüberliegenden Seiten eines regulären Sechsecks mit der Seitenlänge a beträgt , oder anders gesagt, das Doppelte des Inkreisradius
- Der Verkettungsfaktor, das Verhältnis von Phasenspannung (230 V) zu Außenleiterspannung (400 V), beträgt bei Dreiphasenwechselstrom
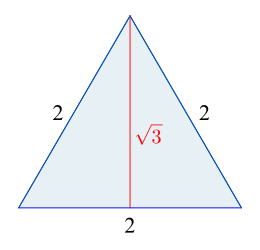
- Die Höhe eines gleichseitigen Dreiecks mit der Seitenlänge a beträgt , sein Flächeninhalt
Weblinks
- Eric W. Weisstein: Theodorus’s Constant. In: MathWorld (englisch).
- Folge A028257 in OEIS (Engel-Entwicklung (englisch Engel expansion) von √3)



































