Sistema d'arrels
En matemàtiques, un sistema arrel és una configuració de vectors en un espai euclidià que satisfà determinades propietats geomètriques. El concepte és fonamental en la teoria de grups de Lie i àlgebres de Lie, especialment en la teoria de la classificació i representació de les àlgebres de Lie semisimples. Atès que els grups de Lie (i alguns anàlegs com els grups algebraics) i les àlgebres de Lie han esdevingut importants en moltes parts de les matemàtiques durant el segle XX, la naturalesa aparentment especial dels sistemes arrels desmenteix el nombre d'àrees en què s'apliquen. A més, l'esquema de classificació dels sistemes arrels, mitjançant diagrames de Dynkin, es produeix en parts de les matemàtiques sense connexió oberta amb la teoria de Lie (com ara la teoria de la singularitat). Finalment, els sistemes arrels són importants per si mateixos, com en la teoria de grafs espectrals.[1]

Història
El concepte de sistema arrel va ser introduït originalment per Wilhelm Killing al voltant de 1889 (en alemany, Wurzelsystem). Els va utilitzar en el seu intent de classificar totes les àlgebres simples de Lie sobre el camp dels nombres complexos. Killing originalment va cometre un error en la classificació, enumerant dos sistemes arrels excepcionals de rang 4, quan de fet només n'hi ha un, ara conegut com F4. Cartan va corregir més tard aquest error, mostrant que els dos sistemes arrels de Killing eren isomòrfics.[2]
Killing va investigar l'estructura d'una àlgebra de Lie , tenint en compte el que ara s'anomena subàlgebra de Cartan . Després va estudiar les arrels del polinomi característic , on . Aquí es considera una arrel en funció de , o de fet com un element de l'espai vectorial dual . Aquest conjunt d'arrels formen un sistema radicular a l'interior , tal com s'ha definit anteriorment, on el producte interior és la forma Killing.
Definicions i exemples
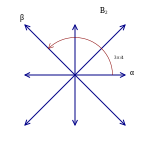
Com a primer exemple, considereu els sis vectors de l'espai euclidià bidimensional, R2, tal com es mostra a la imatge de la dreta; anomenar-los arrels. Aquests vectors abasten tot l'espai. Si considereu la recta perpendicular a qualsevol arrel, per exemple β, aleshores la reflexió de R2 en aquesta línia envia qualsevol altra arrel, per exemple α, a una altra arrel. A més, l'arrel a la qual s'envia és igual a α + nβ, on n és un nombre enter (en aquest cas, n és igual a 1). Aquests sis vectors compleixen la definició següent i, per tant, formen un sistema arrel; aquest es coneix com A2.[3]
 |  |
| Sistema arrel | Sistema arrel |
 |  |
| Sistema arrel | Sistema arrel |
 |  |
| Sistema arrel | Sistema arrel |
Definició
Sigui E un espai vectorial euclidià de dimensió finita, amb el producte interior euclidià estàndard denotat per . Un sistema arrel a E és un conjunt finit de vectors diferents de zero (anomenades arrels) que compleixen les condicions següents:
- Les arrels abasten E.
- Els únics múltiples escalars d'una arrel que pertanyen a són i .
- Per cada arrel , el conjunt es tanca sota la reflexió a través de l'hiperplà perpendicular a .
- (Integralitat) Si i són arrels a , llavors la projecció de a la línia a través és un múltiple enter o mig enter d'.
Una manera equivalent d'escriure les condicions 3 i 4 és la següent:
- Per a dues arrels qualsevol , el conjunt conté l'element
- Per a dues arrels qualsevol , el nombre és un nombre enter.
Alguns autors només inclouen les condicions 1 – 3 en la definició d'un sistema arrel. En aquest context, un sistema arrel que també compleix la condició d'integració es coneix com a sistema arrel cristal·logràfic. Altres autors ometen la condició 2; llavors anomenen sistemes arrels que satisfan la condició 2 reduïda. En aquest article, se suposa que tots els sistemes arrels són reduïts i cristal·logràfics.
A la vista de la propietat 3, la condició d'integralitat equival a afirmar que β i la seva reflexió σ α ( β ) difereixen en un múltiple enter de α. Tingueu en compte que l'operador definit per la propietat 4 no és un producte intern. No és necessàriament simètric i només és lineal en el primer argument.[4]
Referències
- ↑ Cvetković, Dragoš Linear Algebra and Its Applications, 356, 1–3, 2002, pàg. 189–210. DOI: 10.1016/S0024-3795(02)00377-4 [Consulta: free].
- ↑ «[https://users.math.msu.edu/users/ruiterj2/math/Documents/Notes%20and%20talks/Root%20systems.pdf Root systems Joshua Ruiter]» (en anglès). [Consulta: 24 agost 2015].
- ↑ «[https://math.mit.edu/classes/18.745/Notes/Lecture_16_Notes.pdf 18.745 Introduction to Lie Algebras Lecture 16 — Root Systems and Root Lattices]» (en anglès). [Consulta: 24 agost 2015].
- ↑ «ROOT SYSTEMS AND DYNKIN DIAGRAMS» (en anglès). [Consulta: 15 agost 2024].




















